NEB Grade 12 Physics Model Set Solution [Updated 2079] | Nepali Educate

 

XII Physics Model Set Solution

Group A

1. Which of the following is a correct formula for calculating the radius of gyration of a rotating object?
A) k²= I/m
B) k= I/m
C) k= m/I
D) k = (I/m)²

2. A horizontal stream of air is blown under one of the pans of a beam balance as shown in the figure. What will be the effect of this on the pan? 

A) Goes up
B) goes down
C) remains unaffected
D) rotates

3. What will be the height of a capillary on the surface of the Moon if it is „h‟ on Earth?
A) h
B) h/6
C) 6h
D) zero

4. What is the coefficient of performance of an ideal refrigerator working between ice point and room temperature (27°C)?
A) 0
B) 0.1
C) 1
D) 10

5. A thermodynamic system is taken from A to B via C and then returned to A via D as shown in the p-V diagram. The area of which segment of the graph represents the total work done by the system?

A) P₁ACBP₂P₁
B) ACBB’A’A
C) ACBDA
D) ADBB’A’A

6. Which one of the following directly affects the quality of sound?
A) Shape of the source
B) frequency
C) intensity
D) wave form

7. A diffraction pattern is obtained using a beam of red light. What will be the effect on the diffraction pattern if the red light is replaced with white light?
A) All bright fringes become white.
B) All bright fringes, except the central one, become white.
C) All bright fringes become colourful.
D) All bright fringes, except the central one, become colourful.

8. In which one of the following diagrams the currents are related by the equation I₁ – I₂ = I₃ – I₄?

Ans: Option B

9. A coil having N turns and cross-section area A carries current I. Which physical quantity does the product NIA represent?
A) Magnetic flux of the coil
B) magnetic flux density of the coil
C) magnetic moment of the coil
D) magnetic susceptibility of the coil

10. What happens to the neutral temperature if the cold junction of a thermocouple is decreased?
A) Increases
B) Decreases
C) Remains the same
D) Approaches inversion temperature

11. What is the point where the seismic waves start called?
A) Epicentre
B) Hypocentre
C) Metacentre
D) Seismic centre

GROUP B

Short Answer Questions (8 x 5 = 40)

1. (i) Define “surface tension”. [1]

Ans: The property of liquid at rest by virtue of which its surface behaves like a stretched membrane and tries to occupy minimum possible surface area is called surface tension. It is caused by the attractive forces between the molecules of the liquid, which tend to draw the molecules towards the center of the liquid and create a tension on the surface.

(ii) Establish a relation between surface tension and surface energy of a liquid. [2]

Ans: Let us consider a rectangular frame PQRS with length l as shown in figure where QR is movable. When we dip the entire frame in a soap solution, a thin film is formed which tries to pull the wire QR toward the left due to surface tension.

Let T be the surface tension created due to the thin film then force F on QR is due to the surface tension is given by:

F=Tx2l [Note: Some student gets confused with 2, it is because soap film has two surface of contact (inside and outside)]

Again suppose that the wire is moved to Q’R’ with distance x against the surface tension force so as to increase the surface area of the film. Then, the work done is given as:

\[Work\;done{\rm{ }} = {\rm{ }}Force{\rm{ }} \times {\rm{ }}Distance{\rm{ }} = {\rm{ }}F \times 2lx\]

\[Where\;{\rm{ }}2lx{\rm{ }}\;is{\rm{ }}increase{\rm{ }}{\mathop{\rm in}\nolimits} {\rm{ }}the{\rm{ }}surface{\rm{ }}area\]

\[Surface\;{\rm{Energy (}}\sigma {\rm{) =  }}\frac{{Work{\rm{ }}done{\rm{ in increasing surface Area}}}}{{Increase\;{\rm{Surface Area}}}}\]

\[ = \frac{{T \times 2lx}}{{2lx}}\]

\[ = T\]

\[i.e.{\rm{ }}\sigma {\rm{  =  T}}\]

(iii) Two spherical rain drops of equal size are falling vertically through air with a certain terminal velocity. If these two drops were to coalesce to form a single drop and fall with a new terminal velocity, explain how the terminal velocity of the new drop compares to the original terminal velocity. [2]

Ans: It is known that terminal velocity is directly proportional to the square root of the radius of the sphere of sphere and spherical like body.

∴Terminal velocity (v)​α r²

Let r be the radius of small drop and R be radius of large drop.

Equating the volumes:

\[\begin{array}{l}\frac{4}{3}\pi {R^3} = 2(\frac{4}{3}\pi {r^3})\\i.e.R = {2^{\frac{1}{3}}}.r\\And,\\\frac{V}{v} = {(\frac{R}{r})^2} = {2^{\frac{2}{3}}}\\or,V = 1.587v\end{array}\]

Thus, the terminal velocity of large drop is 1.587 times the terminal velocity of small drops.

 

2. Angular speed of a rotating body is inversely proportional to its moment of inertia.
(i) Define „moment of inertia‟. [1]
Ans: Moment of inertia is the sum of the product of the masses of the various particles and the square of their perpendicular distance from the axis of rotation.

(ii) Explain why angular velocity of the Earth increases when it comes closer to the Sun in its orbit. [2]
Ans: As we know angular momentum is L =IѠ. When the earth comes closer to the sun, the moment of inertia of earth decreases about the axis. So to conserve the angular momentum, angular velocity of the earth increases.

(iii) If the Earth were to shrink suddenly, what would happened to the length of the day? Give reason. [2]

Ans: Angular momentum is conserved as there is no external torque.

\[\begin{array}{l}\therefore {L_1} = {L_2}\\i.e.{I_1}{\omega _1} = I{}_2{\omega _2}\\T = \frac{{2\pi }}{\omega }\\\therefore \frac{{{I_1}}}{{{T_1}}} = \frac{{{I_2}}}{{{T_2}}}\\\end{array}\]
∴ On shrinking the earth the moment of inertia will decrease,
∴ Time duration of day will decrease as I∝T

OR

(i) State Bernoulli principle. [1]

Ans: Bernoulli’s theorem states that for the stream line flow of an ideal liquid, the total energy (sum of pressure energy, kinetic energy, and potential energy) per unit mass remains constant at every cross section area throughout the flow.

(ii) Derive Bernoulli‟s equation. [2]
Ans: Let's take a pipe of non-uniform diameter through which a non-viscous liquid flows through it with streamline motion. The liquid is incompressible and its density is $\sigma $. Let A₁, V₁, P₂, and h₁ be the area of cross section, velocity of liquid, pressure of liquid, and height from ground at end A. Similarly, A₂, V₂, P₂, and h₂, be the area of cross section, velocity of liquid, pressure of liquid and be the height from the end B  from the ground.

Let 'm' be the mass of liquid of flowing per second through the pipe.

Then, work done per second on entering the liquid at end A is

${{\rm{W}}_1} = {\rm{force*distance\: per\: second}}$

$ = {{\rm{P}}_1}{\rm{*}}{{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1}$ -------------- (i)

Similarly, work done per second on leaving the liquid at end B

${{\rm{W}}_2} = {{\rm{P}}_2}{\rm{*}}{{\rm{A}}_2}{\rm{*}}{{\rm{V}}_2}$ -------------- (ii)

Now, the difference in energy per second on the flow of liquid is,

$\Delta {{\rm{w}}_1} = {{\rm{w}}_1} - {{\rm{w}}_2}$

$ = {{\rm{P}}_1}{\rm{*}}{{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1} - {{\rm{P}}_2}{\rm{*}}{{\rm{A}}_2}{\rm{*}}{{\rm{V}}_2}$

But, ${{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1} = {{\rm{A}}_2}{\rm{*}}{{\rm{V}}_2}\left( {{\rm{from\: equation\: of\: continuity}}} \right)$

So,

$\Delta {{\rm{w}}_1} = {{\rm{P}}_1}{\rm{*}}{{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1} - {{\rm{P}}_2}{\rm{*}}{{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1}$

$ = \left( {{{\rm{P}}_1} - {{\rm{P}}_2}} \right){\rm{*}}{{\rm{A}}_1}{{\rm{V}}_1}$ ---------- (iii)

But,${{\rm{A}}_1}{\rm{*}}{{\rm{V}}_1} = {\rm{volume\: of\: liquid\: per\: second}} = \frac{{{\rm{mass\: per\: second}}}}{{{\rm{density}}}}$

                                                                                $ = \frac{{\rm{m}}}{\rho }$

Then, equation (iii) gives,

$\Delta {{\rm{w}}_1} = \left( {{{\rm{P}}_1} - {{\rm{P}}_2}} \right){\rm{*}}\frac{{\rm{m}}}{\rho }$ -------------- (iv)

Since, the height h₂ is less than h₁, the potential energy at the end be is less than that of A. So, the last in P.E. per second is 

$\Delta {\rm{P}}.{\rm{E}} = {\rm{p}}.{\rm{e\: per\: second\: at\: A}} - {\rm{p}}.{\rm{e\: per\: second\: at\: B}}$

$ = {\rm{mg}}{{\rm{h}}_1} - {\rm{mg}}{{\rm{h}}_2}$ ----------- (v)

Again, using equation of continuity,

${{\rm{A}}_1}{{\rm{V}}_1} = {{\rm{A}}_2}{\rm{*}}{{\rm{V}}_2}$

Since, A₂ is less than A₁, the velocity V₂ becomes more than V₁. So, there is gain in kinetic energy of the following liquid. Then, the gain in K.E per second is,

$\Delta {\rm{K}}.{\rm{E}} = {\rm{K}}.{\rm{E\: per\: second\: at\: B}} - {\rm{K}}.{\rm{E\: per\: second\: at\: A}}$

$ = \frac{1}{2}{\rm{mv}}_2^2 - \frac{1}{2}{\rm{mv}}_1^2$ ------------ (vi)

For the flow of liquid, the net gain in energy per second is

$\Delta {{\rm{w}}_2} = \left( {\frac{1}{2}{\rm{mv}}_2^2 - \frac{1}{2}{\rm{mv}}_1^2} \right) - \left( {{\rm{mg}}{{\rm{n}}_1} - {\rm{mg}}{{\rm{n}}_2}} \right)$ --------- (vii)

From equation (iv) and (vii), the value of $\Delta {{\rm{w}}_1}{\rm{and\: }}\Delta {{\rm{w}}_2}$ are equal for the conversation of energy. So we have

$\Delta {{\rm{w}}_1} = \Delta {{\rm{w}}_2}$

Or, $\left( {{{\rm{P}}_1} - {{\rm{P}}_2}} \right){\rm{*}}\frac{{\rm{m}}}{\rho } = \left( {\frac{1}{2}{\rm{mv}}_2^2 - \frac{1}{2}{\rm{mv}}_1^2} \right) - \left( {{\rm{mg}}{{\rm{h}}_1} - {\rm{mg}}{{\rm{h}}_2}} \right)$

Or, $\frac{{{{\rm{P}}_1}}}{\rho } - \frac{{{{\rm{P}}_2}}}{\rho } = \frac{{{\rm{V}}_2^2}}{2} - \frac{{{\rm{V}}_1^2}}{2} - {\rm{g}}{{\rm{h}}_1} + {\rm{g}}{{\rm{h}}_2}$

Or, $\frac{{{{\rm{P}}_1}}}{\rho } + \frac{{{\rm{V}}_1^2}}{2} + {\rm{g}}{{\rm{h}}_1} = \frac{{{{\rm{P}}_2}}}{\rho } + \frac{{{\rm{V}}_2^2}}{2} + {\rm{g}}{{\rm{h}}_2}$

In general,

$\frac{{\rm{P}}}{\rho } + \frac{{{\rm{V}}_1^2}}{2} + {\rm{gh}} = {\rm{constant}}$ ------------ (viii)

Equation (viii) is the mathematical expression for Bernoulli's principle

For horizontal pipe, ${{\rm{n}}_1} = {{\rm{n}}_2}$

So, $\frac{{{{\rm{P}}_1}}}{\rho } + \frac{{{\rm{V}}_1^2}}{2} + {\rm{g}}{{\rm{h}}_1} = \frac{{{{\rm{P}}_2}}}{\rho } + \frac{{{\rm{V}}_2^2}}{2} + {\rm{g}}{{\rm{h}}_1}$

Or, $\frac{{{{\rm{P}}_1}}}{\rho } + \frac{{{\rm{V}}_1^2}}{2} = \frac{{{{\rm{P}}_2}}}{\rho } + \frac{{{\rm{V}}_2^2}}{2}$

Or, ${{\rm{P}}_1} + \frac{1}{2}\rho {\rm{v}}_1^2 = {{\rm{P}}_2} + \frac{1}{2}\rho {\rm{v}}_2^2$

In general,

${\rm{P}} + \frac{1}{2}\rho {{\rm{v}}^2} = {\rm{constant\: }}$ ------------ (ix)

Equation (ix) is the expression for Bernoulli's principle for horizontal pipe.

(iii) You can squirt water from a garden hose a considerably greater distance by partially covering the opening with your thumb. Explain how this works. [2]

Ans: Equation of continuity says a₁v₁=a₂v₂. Where ‘a’ and ‘v’ are area and velocity respectively.

From above equation, the speed of flow of water is inversely proportional to the cross sectional are and when the thumb is placed at the opening of the pipe the area decreases and results in increasing speed of the flow of water which leads to cover greater distance.

3. (i) Define “harmonics‟ in music. [1]

Ans: The sound wave which have a frequency that is an integral multiple of a fundamental tone is called harmonics.
(ii) Calculate the frequency of a monotonous sound produced by a 30 cm long flute open at both ends and being played in the first harmonic. [Velocity of sound in air= 330 ms-1] [2]

Ans: Given:
Length of flute (L) = 30cm = 0.3m
Velocity of sound in air (v) = 330m/s
The frequency of the first harmonic (f) is \[\begin{array}{l}f = \frac{v}{{2L}}\\or,f = \frac{{330}}{{2 \times 0.3}}\\Thus,\;{\rm{f  =  550 Hz}}\end{array}\]
(iii) The flute mentioned in question (ii) was being played by a passenger on a stationary bus. The bus then moves uniformly. Explain what change in the pitch of the flute sound, if any, a person sitting on a bench at the bus park will feel when the bus starts moving. [2]

Ans: The apparent frequency of sound heard by stationary observer when the bus starts to move uniformly is:

\[\begin{array}{l}{\rm{f' = }}\,\frac{{v - 0}}{{v + {v_s}}} \times f\\or,f'{\rm{  =  }}\frac{v}{{v + {v_s}}} \times f\end{array}\]

From above equation we can say that the apparent frequency will have low pitch as compared to that of real frequency.

4. (i) State the second law of thermodynamics. [1]

Ans: Kelvin’s states that, “It is impossible to get continuous supply of work from a body by Colling it to a temperature lower than that of its surrounding.”
(ii) A refrigerator transfers heat from a cold body to hot body. Does this not violate the second law of thermodynamics? Give reason. [2]

Ans: The refrigerator is able to transfer heat from the cold body to the hot body by using energy to perform work, which increases the overall entropy of the universe. While this may seem to violate the second law of thermodynamics, it is actually in accordance with the law, because the work performed by the refrigerator increases the overall entropy of the universe, making the final state of the universe more disordered than it was before.
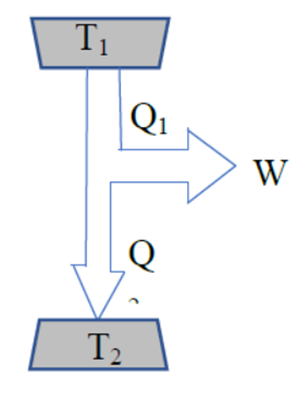
(iii) In the given figure, a heat engine absorbs Q₁ amount of heat from a source at temperature T₁ and rejects Q₂ amount of heat to a sink at temperature T₂ doing some external work W.

(a) Obtain an expression for the efficiency of this heat engine. [1]

Ans: \[\begin{array}{l}Efficiency{\rm{ (}}\eta {\rm{)  =  }}\frac{{External{\rm{ Work Obtained}}}}{{Heat\;{\rm{Energy absorbed From the source}}}}\\\therefore \eta  = \frac{{{Q_1} - {Q_2}}}{{{Q_1}}} \times 100\% \end{array}\]

(b) Under what condition does the efficiency of such engine become zero percentage, if at all? [1]

Ans: For the efficiency to become zero:

i.e. \[\begin{array}{l}\eta  = 0\\or,{\rm{ }}\frac{{{Q_1} - {Q_2}}}{{{Q_1}}} \times 100\%  = 0\\or,{\rm{ }}{Q_1} - {Q_2} = 0\\or,\;{Q_1} = {Q_2}\end{array}\]

5. A student wants to measure the magnetic flux density between the poles of two weak bar magnets mounted on a steel yoke as shown in the figure. The magnitude of the flux density is between 0.02T and 0.04T.
(i) Define Magnetic flux density. [1]

Ans: Magnetic flux density is defined as the force experienced by a charged particle moving through the magnetic field, per unit of charge, per unit of velocity.

Or

The number of magnetic lines of forces acting perpendicular to the area is called magnetic flux density.
(ii) One way of measuring the magnetic flux density could be the use of a Hall probe. Suggest one reason why Hall probe is not a suitable instrument to measure the magnetic flux density for the arrangement shown in the below figure. [1]
Ans: The hall voltage produced by these two bar magnet is very small due to which hall probe is not the suitable device to measure the magnetic flux density for the arrangement shown in the figure below.  

(iii) Another method of measuring the magnetic flux density for the arrangement shown in the above figure is to insert a current-carrying wire between the poles of the magnet. Explain how the magnetic flux density can be determined using this method. You are allowed to use any additional apparatus. [3]

Ans:

 

6. (a) Law of electromagnetic induction can be expressed mathematically as ε = -N(dϕ/dt).

Ans: Law of electromagnetic induction can be expressed mathematically as \[\varepsilon {\rm{ }} =  - N \times \frac{{d\phi }}{{dt}}\]
(b) (i) State what the symbols ε and dϕ/dt represents in the equation. [2]

Ans: ε represent the induced emf and dϕ/dt represent the rate of change of flux.
(ii) Explain the significance of the negative sign. [1]

Ans: The negative sign in the equation is due to Lenz law that is the induced emf is in such a direction to oppose the cause due to which it is produced.
(ii) Two identical copper balls are dropped from the same height as shown in the figure. Ball P passes through a region of uniform horizontal magnetic field of flux density B.
Explain why ball P takes longer than ball Q to reach the ground. [2]