Unit 3 : Atomic Structure | Class 11 Chemistry Complete Notes - Nepali Educate - Educational Resources for Class 11 & 12 Students

ATOMIC STRUCTURE

Rutherford's α-ray scattering experiment and nuclear model

In order to reveal the arrangement of sub atomic particles in an atom, Rutherford and his associate co-worker Geiger and Marsden performed a series of experiment with rays scattering phenomenon on thin gold foil in 1911 which is, therefore, known as Rutherford's α-ray scattering experiment.

In this experiment, a piece of a radioactive substance like radium, uranium etc. was placed in a lead block cavity and a rays produced from radioactive substance were allowed to pass through a slate partition and bombarded on a thin gold foil of about 0.004mm thickness around which a circular moveable ZnS coated screen was adjusted. When the a-rays were scattered on the gold foil, they produced scintillation (flashes of light) on the different portion of screen By examining and observing the different portion of screen, it was became possible to determine the various proportion of x-rays deflected from the gold foil with different angle.

Observations:

From the above experiment, following observations were made:

1. All most all (about 99%) of a- rays passed through the gold foil without any appreciable deflection.

2. Few-rays were deviated with smaller angle than 90°.

3. Very few (1 in 10,000 - 1, 00,000) of the z-rays deviated with extreme larger angle and even renounced back to the original path.

Inference/Conclusion of experiment:

On the basis of above observations, Rutherford came to the following conclusions:

1. Since almost all (99%) of the rays passed through gold foil without any appreciable deflection, it means an atom is almost empty (hollow).

2. Since few α-rays were deviated with small angle than 90", it means they approached near to the positively charged mass concentrated in the nucleus.

3. Since only few (1 in 10,000-1,00,000) a particle were deviated with larger angle and even renounced back to the origin path, it means these particles directly encountered with small but heavy positively charged mass that occupies small space of the nucleus.

From the conclusion of a rays scattering experiment, Rutherford proposed the nucleus model of atom as:

1. Most of the space in the atom is empty.

2. Atom consists of positively charged nucleus at which entire mass is concentrated.

3. Atom is electrically neutral due to equal number of protons and electrons.

4. Nucleus is surrounded by negatively charged electrons which revolve around the nucleus very high speed like solar system.

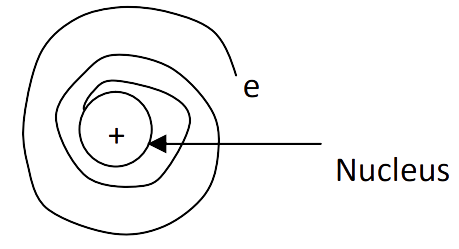
Hence he proposed nuclear model of an atom as given in figure

Limitation of Rutherford's atomic model

1. Stability of an atom:

It could not explain the stability of atom: If an electron revolves around the positively charged nucleus as explained by Rutherford, it losses energy in the form of radiation and its speed decreases due to which its path becomes spirally smaller and smaller. Ultimately the electron falls in to the nucleus. However, it does not happen.

Fig: Spiral path of moving electron

2). It does not explain about emission of atomic spectrum.

Bohr's Atomic Model

In 1913, a German scientist Neils Bohr proposed a new atomic model with new concept in order to overcome the drawbacks of Rutherford's atomic model by applying Planck's quantum theory of radiation which is called Bohr's atomic theory. He retained the main spirit of Rutherford's nuclear model.

The major postulates of Bohr's atomic model are:

1. Stationary State:

Electrons revolve around the nucleus in fixed circular paths at certain distance from the nucleus which are called shells, stationary states, energy levels, orbits which are represented by K, L, M, N.... etc.

2. Numbers of electrons in a shell (2n²formula):

The numbers of electrons that can be hold in a shell is determined by 2n² formula which is called Bohr-Bury rule. Here, n is number of shell.

For example,

Number of electrons in first shell- 2n²=2(1)² Number of electrons in second shell-2(2)²-8

3. Quantization of angular momentum:

Only those orbits are permitted for revolving electrons in which the angular momentum of the revolving electron is equal to whole number multiple of nh/2π these orbits are called Bohr's orbit.

mvr = $\frac{{nh}}{{2\pi }}$

Where,

m: mass of electron

v: velocity of electron

r: radius of orbit

n=Number of shell

h: Planck’s constant(6.626 X 10^-34JS)

4. Origin of spectral line (Atomic spectra):

When electron absorbs energy, it jumps from lower energy level (orbit) to higher energy levels where it is unstable and jumps back to the same lower energy level by emitting energy in the form of light of different wave length that results production of spectral lines. The quantity of absorbed or emitted energy is calculated as:

ΔE = E₂ - E₁

hv= E₂ - E₁

Where,

E₁: energy of electron in first shell

E₂: energy of electron in second shell.

ΔE: absorbed or emitted energy

H: Plank's constant

v: frequency of radiation

5. Balance of electrostatic force of attraction:

Electron revolves around the nucleus in a fixed orbit at certain distance from nucleus is balanced by equal but opposite force i.e. centripetal force and centrifugal force due to which electron doesn't jump into the nucleus.

6. When an electron revolves in a particular orbit, it neither radiates (looses) nor absorbs the energy at ordinary condition.

Outcomes (benefits) Bohr's atomic model

1. It answers successfully about the stability of atom since electron neither losses nor absorbs energy in a particular orbit is balanced by equal and opposite force centripetal and centrifugal force.

2. It explains the origin of atomic spectra in uni-electron system like H, Li⁺⁺ etc.

3. It helps to calculate the energy of the electron in a particular orbit of mono electronic system like hydrogen, lithium. It can be calculated by

$E = {\rm{ }}\frac{{{Z^2}{e^4}m}}{{8{\varepsilon _0}^2{n^2}{h^2}}}$

Where,

ε₀: permittivity of vacuum =8.85 x 1012 Fm^‑1

Z: Atomic number

H: Planck’s constant=6.626 X 10^-34

M: mass of electron (9.1x 10g)

e: charge of electron (-1.6 x10^-19C) n=principal quantum number or number of shell

5).It helps to calculate the radius of the orbit by the relation

$r = \frac{{{\varepsilon _0}{n^2}{h^2}}}{{{\pi ^2}Zm{e^2}}}$

Where

r: radius of orbit

ε₀: permittivity of vacuum

Limitation of Bohr's atomic model:

1. It is significant for the origin of atomic spectra for uni electron system only like H, He", Li" etc but failed for multi electrons system.

2. It does not explain about the splitting of spectral lines in to fine lines in the high resolution power.

3. It doesn't explain about the splitting of spectral line into number of fine lines in the magnetic field (Zeeman Effect) and in the electric field (Stark effect).

4. It fails to explain wave nature of electron.

5. It is against of Heisenberg's uncertainty principle and de-Broglie's equation.

6. It fails to account the three dimensional arrangement of electrons.

7. It is unable to interpret relationship of mvr= $\frac{{nh}}{{2\pi }}$ properly.

Hydrogen spectra in the light of Bohr's theory:

Fig: Hydrogen Spectra

Neils Bohr discovered spectra in uni electron system like H by passing high voltage electricity under reduced pressure. When high voltage electric discharge (10,000Volts) is applied to the hydrogen gas under reduced pressure (0.001atm), hydrogen molecules dissociate into hydrogen atoms at first, Electron of each hydrogen atom absorbs different quantity of energy and jumps from its ground state to different higher energy levels. These excited electrons are unstable at higher energy levels and return back to the ground state either by direct single jump or more successive jumps when the supply of energy cut off. As these excited electrons jumps back to the ground state, they emit energy in the form of radiation having different wave length which results the formation of series of spectral lines. Depending upon the wave length of radiation, five different types of spectral series are recognized.

1. Lyman series:

The spectral series observed when the excited electron jumps from higher energy levels (n₂=2, 3, 4, 5....etc.) to the first energy level (n₁=1) is called Lyman series. It lies in ultraviolet region and wave length of radiation ranges from 920 A° to 1200 A°. Wave number of this series is determined by the relation.

$\begin{array}{l} v = \frac{1}{\lambda } = R(\frac{1}{{n_1^2}} - \frac{1}{{n_2^2}})\\ \frac{1}{\lambda } = R(\frac{1}{{{1^2}}} - \frac{1}{{{2^2}}}) \end{array}$

Where,

λ: Wave length

v: wave number

R: Rydberg's constant =109677/cm

n₁: Lower energy level

n₂: Higher energy level

2. Balmer Series:

The spectral series observed when the excited electron jumps from higher energy levels (n₂=3, 4, 5, 6...etc.) to the second energy level (n₁=2) is called Balmer series. It lies in visible region and wave length of radiation ranges from 4000 A° to 6500 A°. Wave number of this series is determined by the relation.

$\begin{array}{l} v = \frac{1}{\lambda } = R(\frac{1}{{n_1^2}} - \frac{1}{{n_2^2}})\\ \frac{1}{\lambda } = R(\frac{1}{{{2^2}}} - \frac{1}{{{3^2}}}) \end{array}$

3. Paschen series:

The spectral series obtained when the excited electron jumps from higher energy levels (n₂=4, 5, 6, 7....etc.) to the third energy level n₁=3) is called Paschen series. It is observed in Infrared region and wave length of radiation ranges from 9500 A° to 18750 A°. Wave number of radiation of this series is determined by the relation.

$\begin{array}{l} v = \frac{1}{\lambda } = R(\frac{1}{{n_1^2}} - \frac{1}{{n_2^2}})\\ \frac{1}{\lambda } = R(\frac{1}{{{3^2}}} - \frac{1}{{{4^2}}}) \end{array}$

4. Brackett series:

The spectral series obtained when the excited electron jumps from higher = 5, 6, 7...e energy levels (n₂) to the lower energy level (n₁=4) is called Brackett series. It lies in Infrared and wave length of radiation ranges from 19450 A° to 40500A°. Wave length of radiation of this series is determined by the relation.

$\begin{array}{l} v = \frac{1}{\lambda } = R(\frac{1}{{n_1^2}} - \frac{1}{{n_2^2}})\\ \frac{1}{\lambda } = R(\frac{1}{{{4^2}}} - \frac{1}{{{5^2}}}) \end{array}$

5. Pfund Series:

The spectral series observed when the excited electron jumps from higher energy levels (n₂=6, 7....etc.) to the lower energy level (n₁=5) is called Pfund series. It lies in Infra-red and wave length of radiation is above 40500A°. Wave length of radiation of this series is determined by the relation.

$\begin{array}{l} v = \frac{1}{\lambda } = R(\frac{1}{{n_1^2}} - \frac{1}{{n_2^2}})\\ \frac{1}{\lambda } = R(\frac{1}{{{5^2}}} - \frac{1}{{{6^2}}}) \end{array}$

Therefore types of series, range of wavelength and their regions are summarized in the table:

Types of Series	Wave length range	Regions
Lyman	920A^o -1200A^o	UV region
Balmer	4000A^o - 6500A^o	Visible Region
Paschen	9500A^o -18750A^o	Infra-Red Region
Brackett	19450A^o -40500A^o	Infra-Red Region
Pfund	Above 40500A^o	Far Infra-Red Region

Quantum Mechanics:

To overcome the uncertainty of Bohr’s atomic model this theory was developed. This theory become successful to explain the wave particle nature of the electron.

1. De Broglie Wave Equation:

De-Broglie extended the idea of dual nature of light to matter particle and suggested that all matter particle in motion shows dual nature i.e. particle and wave nature. It means electron shows the characteristics of wave as well as particle.

De Broglie Wave Equation: λ= $\frac{h}{{mv}}$

2. Heisenberg Uncertainty Principle:

Statement: It states that it is impossible to determine the position and momentum of microscopic particle in motion simultaneously and accurately.

Mathematically: Δx. Δp > $\frac{h}{{4\pi }}$

Where,

Δx: Uncertainty in Position

Δp: Uncertainty in Momentum

3. Schrödinger’s Wave Mechanics:

Statement: The wave particle duality of electron has laid foundation of wave mechanics model of an atom. He derived a complicated mathematical equation. Considering an atom as positively charged nucleus surrounded by stationary electron wave which extends around the nucleus in Bohr’s circular orbit. In this model electron is considered as three dimensional wave in electronic field of positively charged nucleus.

Difference between orbit and orbital:

Orbit	Orbital
It is well defined circular path where electron revolves around nucleus.	It is the three dimensional space where the probability of finding electron is maximum.
The concept was developed from Bohr’s Atomic Model.	The concept was developed from Heisenberg uncertainty principle.
Orbit use two dimensional concept.	Orbital use three dimensional concept.
They are non-directional character.	They use directional character.
One orbit can accommodate maximum 2n² number of electron.	One orbital can accommodate only two electron.

Quantum Numbers:

Those number which gives complete information about the motion and location of an electron in an atom is called quantum numbers.

There are altogether four quantum numbers.

i. Principle Quantum Number (n):

It represent Bohr’s orbit and denotes major shell to which the electron belongs. The value of n is non-zero positive integers and is equal to 1, 2, 3, 4… or K, L, M, N…. respectively.

The maximum number of electron that a shell can hold is given by 2n²rule.

Example:

For K shell: maximum number of electron = 2n² = 2×1²=2

ii. Azimuthal Quantum Number(L):

It represent the number of subshell by which a shell is composed of. The value of L is equal to 0, 1, 2, and 3 for s, p, d and f orbitals respectively. Its value ranges from 0 to (n-1).

The maximum number of electron that a shell can hold is given by 2n (2L +1) rule.

Example:

For s-subshell: maximum no. of electron = 2n (2L +1) = 2×1 (2×0 +1) =2

Note:

S àSharpe

P à Principle

D àDiffused

F à Fundamental

iii. Magnetic Quantum Numbers (M):

It helps to determine the orientation of orbitals in space. The maximum number of electron that an orbital can hold is 2.The value of M range from –L to L including 0.

Example:

For s-subshell: L= 0 and M= -0 to +0 i.e. 0. It means s subshell consist of single orbitals.

For p-subshell: L=1 and M = -1 to 1 i.e. -1, 0, 1. It means p-subshell consist of three orbital i.e. p_x, p_y, p_z

iv. Spin Quantum Number (s):

While revolving around nucleus electron circulates in its own axis either in clockwise or in anticlockwise direction which gives information about the spin quantum number.

Example:

S=½ à clockwise direction

S=-½à anticlockwise direction

Electronic Configuration (nL^x):

1. Afbau Principle:

It states that, “While filling electrons in atomic orbitals, first filled up to the orbitals having lower energy than only filled up to the orbitals having high energy.”

Fig. Filling Sequence of electron in increasing of energy level

1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,….

The orbital with lower (n + L) value have lower energy and is filled first than the orbital with higher energy.

Example: 2s orbital is filled earlier than 2p orbital because 2s has lower (n +L) value than 2p orbital.

n+ L for 2s = 2+0=2

n + L for 2p = 2+1=3

If the orbital have same (n + L) value than the orbital with lower n value is filled first.

Example: 3d orbital is filled earlier than 4p orbital because 3d has lower value of n than 4p.

Electronic Configuration of Element from 1 to 30:

Atomic Number	Name of the Element	Electronic Configuration
1	Hydrogen (H)	1s¹
2	Helium (He)	1s²
3	Lithium (Li)	[He] 2s¹
4	Beryllium (Be)	[He] 2s²
5	Boron (B)	[He] 2s² 2p¹
6	Carbon (C)	[He] 2s² 2p²
7	Nitrogen (N)	[He] 2s² 2p³
8	Oxygen (O)	[He] 2s² 2p⁴
9	Fluorine (F)	[He] 2s² 2p⁵
10	Neon (Ne)	[He] 2s² 2p⁶
11	Sodium (Na)	[Ne] 3s¹
12	Magnesium (Mg)	[Ne] 3s²
13	Aluminum (Al)	[Ne] 3s² 3p¹
14	Silicon (Si)	[Ne] 3s² 3p²
15	Phosphorus (P)	[Ne] 3s² 3p³
16	Sulphur (S)	[Ne] 3s² 3p⁴
17	Chlorine (Cl)	[Ne] 3s² 3p⁵
18	Argon (Ar)	[Ne] 3s² 3p⁶
19	Potassium (K)	[Ar] 4s¹
20	Calcium (Ca)	[Ar] 4s²
21	Scandium (Sc)	[Ar] 3d¹ 4s²
22	Titanium (Ti)	[Ar] 3d² 4s²
23	Vanadium (V)	[Ar] 3d³ 4s²
24	Chromium (Cr)	[Ar] 3d⁵ 4s¹
25	Manganese (Mn)	[Ar] 3d⁵ 4s²
26	Iron (Fe)	[Ar] 3d⁶ 4s²
27	Cobalt (Co)	[Ar] 3d⁷ 4s²
28	Nickel (Ni)	[Ar] 3d⁸ 4s²
29	Copper (Cu)	[Ar] 3d¹⁰ 4s¹
30	Zinc (Zn)	[Ar] 3d¹⁰ 4s²

Electronic Configuration of IONS:

Ca⁺⁺:1s²2s²2p⁶3s²3p⁶

Mg⁺⁺:1s²2s²2p⁶

Fe⁺:1s²2s²2p⁶3s²3p⁶4s¹3d⁶

Fe⁺⁺:1s²2s²2p⁶3s²3p⁶3d⁶

Fe⁺⁺⁺:1s²2s²2p⁶3s²3p⁶3d⁵

2. Pauli’s Exclusion Principle:

It states that “No two electron of an atom has same set of all four quantum number.”

Illustration: The quantum number of two electron of helium are:

No. of electron	n	L	m	s
1^st electron	1	0	0	+½
2^nd electron	1	0	0	-½

3. Hund’s Rule of Maximum Multiplicity:

It states that, “In the orbitals of same subshell electron are filled singly first, before paring starts up.”

Electron are arranged themselves in degenerated orbitals. So, as to retain parallel spin quantum numbers. Electrons of same charge repels each other and tends to satay apart from each other as far as possible. That means electron enter degenerated orbitals, this minimizes inter electronic repulsion and the system will be more stable due lowering of energy. Thus Hund’s rule accounts extra stability of electronic configuration.

Importance of Hund’s Rule:

According to Hund’s rule two electron in same orbital have different spin quantum number. This verifies exclusion principle.

This rule is applicable for knowing the electronic configuration in more expanded form.

Bohr Bury Rule:

In 1921 Bohr's Bury proposed a scheme for the distribution of electrons in different orbits in an atom of the element is called Bohr's bury scheme.
The main points of this scheme are:
The maximum number of electrons that and hold is given by 2n² rule. Where n is the number of shells. Therefore k shell poses 2 electrons, L shell poses 8 electrons, M shell poses 18 electrons, and N shell poses 32 electrons.
The maximum number of electrons in the outer orbit is 8 and next to the outer most orbit that is penultimate orbit is 18.

Example:

Element	Atomic No.	K	L	M	N	O
Kr	36	2	8	18	8
Xe	54	2	8	18	18	8

It is not necessary for an orbit to be completely filled before the next orbit starts filling. In fact, new orbit starts electron filling when outermost orbit get 8 electron.

Example:

Element	Atomic No.	K	L	M	N
Na	11	2	8	1
K	19	2	8	8	1

Unit 3 : Atomic Structure | Class 11 Chemistry Complete Notes

ATOMIC STRUCTURE

Rutherford's α-ray scattering experiment and nuclear model

Observations:

Inference/Conclusion of experiment:

Limitation of Rutherford's atomic model

Bohr's Atomic Model

The major postulates of Bohr's atomic model are:

Outcomes (benefits) Bohr's atomic model

Limitation of Bohr's atomic model:

Hydrogen spectra in the light of Bohr's theory:

1. Lyman series:

2. Balmer Series:

3. Paschen series:

4. Brackett series:

5. Pfund Series:

Quantum Mechanics:

1. De Broglie Wave Equation:

2. Heisenberg Uncertainty Principle:

3. Schrödinger’s Wave Mechanics:

Difference between orbit and orbital:

Quantum Numbers:

i. Principle Quantum Number (n):

ii. Azimuthal Quantum Number(L):

iii. Magnetic Quantum Numbers (M):

iv. Spin Quantum Number (s):

Electronic Configuration (nLx):

1. Afbau Principle:

Electronic Configuration of Element from 1 to 30:

2. Pauli’s Exclusion Principle:

3. Hund’s Rule of Maximum Multiplicity:

Bohr Bury Rule:

Post a Comment

Electronic Configuration (nL^x):