NEB 2079 Grade 12 Physics Exam Paper Solution

Group 'A'

Rewrite the correct options of each question in your answer sheet.

1. In rotational motion, the physical quantity that imparts angular acceleration is,

(A) Force

(B) Torque

(C) Moment of inertia

(D) Angular momentum

Ans: Option B: Torque

2. Two identical springs are arranged with a block as in figure. The oscillation frequency of the mass is 'f'. If one spring is removed, the frequency of the oscillation will be,

$\begin{array}{l}(A)f\\(B)2f\\(C)\sqrt {2f} \\(D)\frac{f}{{\sqrt 2 }}\end{array}$

Ans: Option d: $\frac{f}{{\sqrt 2 }}$

3. A liquid does not wet the surface of a solid if the angle of contact is,

(A) 90°

(B) less than 90°

(C) greater than 90°

(D) 0°

Ans: Option C: Greater than 90°

4. Identify the wrong statement

(A) for isothermal process, ΔT = 0

(B) for isochoric process, ΔV= 0

(C) for isobaric process, ΔP = 0

(D) for cyclic process, ΔW = 0

Ans: Option D: for cyclic process, triangle ΔW = 0

5. The maximum efficiency of an engine operating between 30°C and 300°C is,

(A) 4.71%

(B) 47%

(C) 90%

(D) 9%

Ans: Option B: 47%

6. In which frequency range the infrasonic wave lies?

(A) (10-20) Hz

(B) (30-40)Hz

(C) (20-30) Hz

(D) (50-60) Hz

Ans: Option A:(10-20) Hz

7. In Fraunhofer diffraction, the incident wave front should be,

(A) elliptical

(B) plane

(C) spherical

(D) cylindrical

Ans: Option B: Plane

8. If specific resistance of a potentiometer wire is 10 ^{- 7}Ωm, current flowing through it is 0.1A and cross-sectional area of wire is 10^{- 6}m², then potential gradient will be,

(A) 10^-2 V / m

(B) 10^-4V / m

(C) 10^{- 6}V / m

(D) 10^{- 8}V / m

Ans: Option A: 10^-2 V / m

9. A coil having N-number of turns and cross-section area A carries a current 1. The quantity NIA is,

(A) magnetic flux

(B) magnetic field

(C) magnetic susceptibility

(D) magnetic moment

Ans: Option D: magnetic moment

10. At resonance, in series LCR circuit, which relation does not hold good,

$\begin{array}{l}(A)\;\omega  = \frac{1}{{\sqrt {LC} }}\\(B)L\omega  = \frac{1}{{C\omega }}\\(C)C\omega  = \frac{1}{{L\omega }}\\(D)\omega  = \frac{1}{{LC}}\end{array}$

Ans: Option A: $\frac{1}{{\sqrt {LC} }}$

11. Which of the following one is correct?

(A) E² = P²C

(B) E² = P²C²

(C) E²= PC²

(D) E²= P² / C²

Ans: Option B: E² = P²C²

Group 'B'

12. The angular speed is inversely proportional to the moment of inertia, that is given by the principle of conservation of energy.

a) In a flywheel, most of the mass is concentrated at the rim. Explain why?

Ans:

A flywheel has most of its mass concentrated at the rim to increase its moment of inertia and store more kinetic energy for a given angular velocity. This allows it to better regulate the speed of a machine or system, especially in machines that experience fluctuations in power or speed.

b) The angular velocity of the earth around the sun increases when it comes closer to the sun. Why?

Ans:

The angular velocity of the Earth around the sun increases when it comes closer to the sun due to the conservation of angular momentum. The gravitational force between the two bodies increases as the Earth moves closer to the sun, resulting in a net torque on the Earth that causes it to speed up and increase its angular velocity. Similarly, when the Earth moves away from the sun, the gravitational force decreases, resulting in a decrease in its angular velocity.

c) If the earth were to shrink suddenly, what would happen to the length of the day?

Ans:

If the Earth were to shrink suddenly, the length of the day would decrease because the principle of conservation of angular momentum governs the Earth's rotation. As the Earth's moment of inertia decreases due to shrinking, but its angular momentum remains constant, its angular velocity would increase, leading to shorter days.

13. Simple harmonic motion is defined from periodic functions like sine or cosine functions,

a) State the basic equation of motion for a body executing simple harmonic motion.

Ans:

  When a heavy metallic bob is connected at one end of a light, inextensible thread and the thread passes through a frictionless rigid support so that the bob can oscillate in a fixed vertical plane. Then the device is called simple pendulum.

Let us consider a body of mass ‘m’ is connected at one end of a thread of length ‘l’ which passes through a rigid support at point O.

Here,

The point O on the rigid support is called point of suspension and c.g. of the bob is called point of oscillation.

The distance between point of suspension and oscillation is called effective length.

At extreme position, let, mg is the wt. of the body and T be the tension produced in the string. The component mgcos$\theta $ is balanced by the tension (T).

The component mgsin$\theta $ provides restoring force to move the bob towards mean position.

∴ f = -mgsin$\theta $ , -ve sign is for restoring force.

or, ma = -mg sin$\theta $

or, a = -g sin$\theta $

for small angle, sin$\theta $$ \approx $$\theta $

a = -g$\theta $  --------------i)

By trigonometry,

$\theta $ = $\frac{{{\rm{arc\: length}}}}{{{\rm{radius}}}}$ = $\frac{{{\rm{AB}}}}{{{\rm{OA}}}}$

$\theta $ = $\frac{{\rm{y}}}{{\rm{l}}}$  ----------------ii)

Putting the value of $\theta {\rm{\: }}$in eqn ii) we get,

a = -g $\frac{{\rm{y}}}{{\rm{l}}}$

a = -($\frac{{\rm{g}}}{{\rm{l}}}$)y  ---------------iii)

Here, acceleration is directly proportional to displacement, and they are opposite to each other.

Hence, motion of a simple pendulum is SHM

b) Find expression for velocity and acceleration of a particle describing SHM.

Ans:

Displacement of a body in S.H.M. X=Acos(ωt+ϕ).

i) Displacement(x): At t=0 displacement x=A i.e., extreme position when ωt=ϕ=90∘ displacement x=0 at mean position at any point x=Acos(ωt+ϕ).

ii) Velocity (V): Velocity of a body in S.H.M. is V=$ \begin{array}{l}\frac{{dx}}{{dt}} = \frac{d}{{dt}}(Acos\left( {\omega t + \phi } \right))\\\therefore V = {\rm{ }} - A\omega sin(\omega t + \phi )\end{array}$

iii)Acceleration (a): Acceleration of a body in S.H.M. is  $\begin{array}{l}a = \frac{{dv}}{{dt}} = \frac{d}{{dt}}({\rm{ }} - A\omega sin(\omega t + \phi ))\\ =  - A{\omega ^2}cos(\omega t + \phi ) =  - {\omega ^2}x\end{array}$

c) The tip of tuning fork goes through 550 complete vibrations in 1 sec. Find the angular frequency and time period of the motion.

Ans:

The tuning fork vibrates 550 times in 1 seconds.

Then, Frequency (f) = 550/1 = 550Hz

We Know,

Angular Frequency(ω) = $\frac{f}{{2\pi }} = \frac{{550}}{{2\pi }} = 87.53$

OR

a) Define surface tension.

Ans:

The property of liquid by virtue of which it tries to occupy minimum surface area within the given volume is called surface tension.

b) State Bernoulli's theorem.

Ans:

It states that in a steady flow of an incompressible fluid, the total energy of the fluid remains constant along any streamline, where "total energy" is the sum of the fluid's kinetic energy, potential energy, and pressure energy.

c) Castor oil at 20°C has a coefficient of viscosity 2.42Nsm^-2 and density 940kgm^-3. Calculate the terminal velocity of a steel ball of radius 2mm falling under the gravity in the oil, taking the density of steel as 7800kg /m³. (g = 10m /s²)

Ans:

Given,
Here coefficient of viscosity of castor oil (η)=2.42Ns/m²
Density of the oil (σ)=940kg/m³
Radius of the steel ball (r)=2mm=0.002m
Density of the steel (ρ)=7800kg/m³
Terminal velocity (v)=?

We Know:

When the steel ball falls downward with terminal velocity (v), then
Total upward force = Total downward force
Viscous force (F) + Upthrust (U) = Weight of the steel ball (W)

F=W−U

$\begin{array}{l}6\pi \eta rv = \frac{4}{3}\pi {r^3}\rho g - \frac{4}{3}\pi {r^3}\sigma g\\by{\rm{ Solving,}}\;{\rm{We Get:}}\\v = \frac{{2{r^2}(\rho  - \sigma )g}}{{9\eta }} = \frac{{2{{(0.002)}^2} \times (7800 - 940) \times 10}}{{9 \times 2.42}}\; = 0.025m/s\end{array}$

14. Adiabatic process:

a) Define adiabatic process in thermodynamics.

Ans:

An adiabatic process is a thermodynamic process in which there is no exchange of heat between the system and its surroundings. In other words, the system is thermally isolated, and there is no transfer of heat energy as the process occurs.

b) Derive expression for work done during adiabatic process.

Ans:

Consider one mole of ideal gas is enclosed in a cylinder having non-conducting walls and fitted with moveable and frictionless piston.

Let${\rm{\: }}{{\rm{P}}_1}{\rm{\: }}{{\rm{V}}_1}{\rm{\: and\: }}{{\rm{T}}_1}$ are the initial state of the gas in the cylinder. Let, the gas expand from its initial volume V₁ to final volume V₂.

Then, the work done by the is given by,

W = $\mathop \smallint \limits_{{{\rm{V}}_1}}^{{{\rm{V}}_2}} {\rm{Pdv}} \ldots  \ldots  \ldots  \ldots  \ldots 1$

For the adiabatic process, ${\rm{P}}{{\rm{V}}^{\rm{w}}} = {\rm{constant\: }}\left( {\rm{K}} \right)$

${\rm{or}},{\rm{\: P}} = \frac{{\rm{k}}}{{{{\rm{V}}^{\rm{w}}}}}$

Now, substituting the value of P in equation 1 we get

W = $\mathop \smallint \limits_{{{\rm{V}}_1}}^{{{\rm{V}}_2}} \frac{{\rm{K}}}{{{{\rm{V}}^{\rm{w}}}}}{\rm{dv}}$

   $\frac{{\rm{K}}}{{1 - {\rm{w}}}}\left[ {{\rm{V}}_2^{1 - {\rm{w}}} - {\rm{V}}_1^{1 - {\rm{w}}}} \right]$

$\frac{{\rm{K}}}{{1 - {\rm{w}}}}\left[ {{\rm{KV}}_2^{1 - {\rm{w}}} - {\rm{KV}}_1^{1 - {\rm{w}}}} \right] \ldots  \ldots  \ldots .2$

Since, we have,

${{\rm{P}}_1}{\rm{\: V}}_1^{\rm{w}} = {\rm{\: }}{{\rm{P}}_2}{\rm{\: V}}_2^{\rm{w}} = {\rm{K}}\left( {{\rm{constant}}} \right)$

Here from 2

${\rm{W}} = \frac{1}{{1 - {\rm{w}}}}\left( {{{\rm{P}}_1}{\rm{\: }}{{\rm{V}}_1} - {\rm{\: }}{{\rm{P}}_2}{\rm{\: }}{{\rm{V}}_2}} \right) \ldots  \ldots  \ldots .3$

For one mole of ideal gas,

Pv +RT

${\rm{W}} = \frac{{\rm{R}}}{{1 - {\rm{w}}}}\left( {{{\rm{T}}_1}{\rm{\: }} - {\rm{\: }}{{\rm{T}}_2}{\rm{\: }}} \right) \ldots  \ldots  \ldots .4$

This equation 3 and 4 gives the work done is the work done during adiabatic process.

c) Write the mathematical expression of entropy.

Ans:

The mathematical expression for entropy is:

\[\Delta S = Q\left( {\frac{1}{{{T_2}}} - \frac{1}{{{T_1}}}} \right)\]

15. a) Define an organ pipe.

Ans:

A pipe open at both ends is called an open organ pipe.

Example: Flute

b) Describe the various modes of vibration of the air column in a closed organ pipe.

Ans:

Various Modes of vibrations of air column in a closed pipe:

• The air at the closed end is not free to vibrate so a node is formed at the closed end.
• While the air at the open end is free to vibrate with maximum amplitude so an antinode is formed at this end.
• This is the simplest mode of vibration and is called fundamental mode.

\[\begin{array}{l}L = \frac{\lambda }{4} \to 4L = \lambda \\Frequency({f_1})\,{\rm{ =  }}\frac{v}{\lambda } = \frac{v}{{4L}}\end{array}\]

were,

v is the velocity of sound in air,

L is the length of the vibrating column,

λ is the wavelength.

Second mode: or first overtone — [Figure (2)]

\[\begin{array}{l}L = \frac{{3\lambda }}{4} \to \lambda  = \frac{{4L}}{3}\\Frequency({f_2})\,{\rm{ =  }}\frac{v}{\lambda } = \frac{{3v}}{{4L}}\end{array}\]

Similarly for third mode or second overtone [figure (3)]

\[\begin{array}{l}L = \frac{{5\lambda }}{4} \to \lambda  = \frac{{4L}}{5}\\Frequency({f_3})\,{\rm{ =  }}\frac{v}{\lambda } = \frac{{5v}}{{4L}}\end{array}\]

Thus, ${f_1}:{f_2}:{f_3} = 1:3:5$

c) What is end correction?

Ans:

The distance between Anti Node and the open end of a organ pipe is called end correction.

OR

a) State Doppler's effect.

Ans:

The Doppler effect is a phenomenon in physics that describes the apparent change in frequency of a wave, such as sound or light, when the source of the wave is moving relative to an observer.

b) Derive the apparent frequency of sound when an observer moves towards a stationary source.

Ans:

When the source of the sound moves towards the static observer, wavelength of sound decreases which results to increase in frequency of sound.

 \[\begin{array}{l}\lambda '{\rm{  =  }}\frac{{v - {u_s}}}{f}\\If\;{\rm{f'\; be\; the\; apparent\; change\; in\; frequency,\; then\;}}\end{array}\]\[f' = \frac{vf}{{\lambda '}} = \frac{v}{{v - {u_s}}}\]v= Velocity of sound

u_s= Velocity source

λ’ = changed wavelength

f= frequency of sound

since,

v>v- u_s

i.e. f’>f

So, frequency increases when source wave is towards the observer in rest.

c) A stationary motion detector sends sound waves of 150 KHz towards a truck approaching at a speed of 120km/hr. What is the frequency of wave reflected back to detector? (Velocity of sound in air =340m/s)

Ans:

Given:

Frequency of sound wave = 150 Kilo-Hz

speed of the truck = 120 km/hr.

velocity of sound in air = 340 m/s

To find:

The frequency of wave reflected back to detector.

Solution:

Now, frequency of wave reflected back (f) = f_s x (u + u_o)/(u – u_s)

where, u = speed of sound,

       (u)o = initial speed

        (u)s = final speed.

Here, u = 340m/s

initial speed of the truck = 0m/s.

speed of truck = 120 km/hr.

to convert km/hr. into m/s we multiply it with (5/18)

                       = 120 x (5/18)

                       = 33.333 m/s

f = f_s x (u + u_o)/(u - u_s)

   = fs x (340 - 0)/(340 - 33.333)

   = 150,000(340)/(306.667)

   = 166,304.16 Hz

   = 166.304 Kilo-Hz

The frequency of wave reflected back to detector would be 166.304 Kilo-Hz.

16. a) Differentiate See beak's effect and Peltier's effect.

Ans:

Seebeck Effect	Peltier Effect
Temperature difference in dissimilar metals/semiconductors results in electric current.	Temperature difference created across junction of dissimilar conductors results in heat transfer.
Effect is reversible.	Effect is reversible.
Direction of current flow and voltage polarity depends on temperature difference.	Direction of heat flow and voltage polarity depends on current flow.
Used in thermocouples to measure temperature.	Used in thermoelectric coolers and heaters.
Measured by Seebeck coefficient.	Measured by Peltier coefficient.

 

b) Explain the variation of thermo-emf with temperature.

Ans:

Variation of thermos-EMF with temperature:

To study the variation of thermo-emf with temperature, an iron copper thermocouple is taken as shown in the figure. One junction has emerged in an oil bath and the other junction is kept at melting ice most temperature is kept constant. The temperature of the oil bath is increased gradually by heating it.

When the temperature of the hot junction is increased and the cold junction is kept at 0 degree Celsius the deflection on the galvanometer increases that is EMF also increases till it becomes maximum at θ_n neutral temperature.
As the temperature of the hot junction is increased beyond neutral temperature thermos-EMF starts to decrease and ultimately becomes zero at θ_i temperature called as temperature of inversion.
If the temperature is increased beyond θ_i the direction of thermos-emf is reversed. The inversion temperature depends upon the temperature of cold junction and nature of metal used in thermocouple.
The variation of thermos-emf with temperature is shown in the figure given below

Diagram: Variation of EMF with Temperature

The variation of thermos-emf with temperature is given by the expression:
\[E = \alpha \theta  + \frac{1}{2}\beta {\theta ^2}\]

Where α and β are constant and their value depend upon the material of the conductor and the temperature difference between the junctions.

If θ_c be the temperature of the cold junction. Then we have

\[{\theta _{i\;}}--{\rm{ }}{\theta _{{\bf{n}}\;}} = \;{\theta _{\bf{n}}}\; - {\rm{ }}{\theta _{\bf{c}}}\]

\[{\theta _{n\;}} = {\rm{ }}\frac{{({\theta _i} + {\rm{ }}{\theta _c})}}{2}\]

17. When a charge particle moves in a uniform magnetic field, it experiences a force, called the Lorentz force.

a) What is the vector representation of Lorentz force?

Ans:

Vector Form of Lorentz force is:

$\overrightarrow F  = q(\overrightarrow v  \times \overrightarrow B )$

where F is the force experienced by the particle, q is the charge of the particle, E is the electric field, v is the velocity vector of the particle, and B is the magnetic field.

b) State Fleming left hand rule.

Ans:

It states that if the thumb, forefinger, and middle finger of the left hand are held mutually perpendicular to each other, then the thumb points in the direction of the force, the forefinger points in the direction of the magnetic field, and the middle finger points in the direction of the current.

c) A horizontal straight wire 5 cm long weighing 1.2gm is placed perpendicular to a uniform horizontal magnetic field of flux density 0.6T. If the resistance of the wire is 3.82Ωm^-1, calculate the p.d. that has to be applied between the ends of the wire to make it just self-supporting.

Ans:

 Ans:

Here,

Length of the wire, (l) = 5cm = 0.05 m

Mass per unit length of the wire = 1.2 g m^-1 = 1.2 x 10 ^-3 kg m^-1

Magnetic flux density, B = 0.6T

Resistance per unit length of the wire = 3.8Ωm^-1

Acceleration due to gravity, g = 9.8ms^-2

P.d. to be applied, V = ?

We know,

Mass of the wire, m = mass per unit length x length of the wire

Or, m = 1.2 x 10^{- 3}0.05kg

∴ m = 6 x 10^-5 kg

Resistance of the wire, R = Resistance per unit length x Length of the wire

Or, R = 3.8 * 0.05 , R = 0.19Ω

Thus,

F = BIl

$\begin{array}{l}or,\;mg = B\frac{V}{R}l\\or,{\rm{ V = }}\frac{{mgR}}{{Bl}} = \frac{{6 \times {{10}^ - }5 \times 9.8 \times 0.19}}{{0.6 \times 0.05}}\\\therefore V = 3.720 \times {10^{ - 3}}\;{\rm{volt}}\end{array}$

18. Electron is deviated in electric and magnetic fields.

a) What path does the electron follow in electric field when the electron is projected normally in the field?

Ans:

When it is projected normally to the electric field, it follows parabolic path.

b) An electron passes through a space without deviation. Does it mean, there is no fields?

Ans:

No, it does not necessarily mean that there are no fields present. It is possible that the electron is passing through a region where there are electric or magnetic fields present, but the direction and magnitude of these fields are such that they do not cause the electron to deviate from its path.

c) Is there any condition that an electron does not experience any force inside the magnetic field?

Ans:

The force experienced by the electron may be zero if the electron is moving parallel to the magnetic field lines. In this case, the Lorentz force acting on the electron will be perpendicular to its direction of motion and hence it will not experience any net force along its direction of motion.

19. a) What is rectification?

Ans:

The process of converting an ac signal into dc signal is called rectification. An electronic device which converts a.c. power into d.c. power is called a rectifier. 

b) Explain rectifier circuit operation with two diodes.

Ans:

Arrangement

The a.c. supply is fed across the primary coil (P) of step-down transformer. The two ends of S–coil (secondary) of transformer is connected to P-section of junction diodes D₁ and D₂. A load resistance RL is connected across the n–sections of two diodes and central tapping of secondary coil. The d.c. output is obtained across R_L. 

Theory

During first half of input cycle upper end of s-coil is at +ve potential. The junction diode D₁ gets forward biased, while D₂ gets reverse biased. The conventional current due to D₁ will flow along path of full arrows. When second half of input cycle comes, the conditions will be exactly reversed. Now the junction diode D₂ will conduct, and the conventional current will flow along path of dotted arrows.

Since current during both the half cycles flows from right to left through load resistance R_L, the output during both the half cycles will be of same nature.

The right end of R_L is at +ve potential w.r.t. left end. Thus, in full wave rectifier, the output is continuous.

c) What happens when one of the diodes becomes functionless?

Ans:

If one of the diodes in a full-wave rectifier circuit becomes functionless or fails, the circuit will continue to function, but the output waveform will be distorted. Specifically, when one of the diodes fails, it will essentially act as an open circuit, allowing current to flow through the other diode in only one direction, producing a half-wave rectified output.

Group 'C'

20. a) Write sustainable conditions for interference?

Ans:

1. The two sources of waves must emit waves of the same frequency and wavelength.
2. The waves emitted by the sources must be coherent, meaning that they have a constant phase difference between them.
3. The waves must travel through a medium that is uniform and of the same density.

b) "The bright and dark fringes are equally spaced." Justify this statement from Young's double slit experiment.

Ans:

Suppose the light waves from the slate S₁ and S₂ meet at any point P on the screen. Point p will be either maxima or minima depending on the path difference.

Where,
D is the distance between source and screen,
d is separation of sheet and
y is the position of the pattern from the center of the screen.

From the figure,
Path difference, (∆x) = S₂P₁ - S₁ P₁.......(1)

In ∆S2PN:
S₂P² =D²+ (y+d/2)².......(2)

In ∆S1PM,

S₁P²= D²+ (y-d/2)².............(3)
Solving equation 2 and 3,
S₂P²-S₁P²=2yd
(S₂P-S₁P)(S₂P+S₁P)=2yd
(S₂P-S₁P)=2yd/(S₂P+S₁P)
(S₂P-S₁P)=2yd/2D             [∵, S₁P ≈ S₂P ≈ D]
Thus, x = yd/D..........(4)

For Maxima:
x = n λ and from equation 4,

i.e., n λ = yd/D

or, y= n λD/d

Put n=2 and n= 1and subtract.

β_bright=y₂-y₁ = λD/d ………………. (5)

Where, β_bright is the distance between two consecutives bright pattern.

For Minima:
x=(2n+1)  and from equation 4,

i.e., (2n+1)= yd/D

or, y=(2n+1) 

Put n=2 and n= 1and subtract.

β_dark=y₂-y₁ = λD/d …… (6)

Where, β_dark = is the distance between two consecutives dark pattern.

From equation 5 and 6 it is clear that the wheats of bright and dark patterns during interference are equal called fringe width.

c) In a Young's slits experiment the separation of first to fifth fringes is 2.5 mm when the wavelength used is 620 nm. The distance from the slits to the screen is 80 cm. Calculate the separation of two slits.

Ans:

Given,

The wavelength of light (λ) =620nm=6.2×10⁻⁷m

Distance between the slits and screen (D) = 80 cm = 0.8 m,

Separation of slits (d) =?

Separation of four bright fringes (y) = 3β = 2.5 x 10^-3m

We Know,

\[\begin{array}{l}\beta  = \frac{{\lambda D}}{d}\\and\\y = 3\beta  = \frac{{3\lambda D}}{d}\\{\rm{Or, d = }}\frac{{3\lambda D}}{\beta }\,\\or{\rm{, d = }}\frac{{3 \times 6.2 \times {{10}^{ - 7}} \times 0.8}}{{2.5{\rm{ }}x{\rm{ }}{{10}^{ - 3}}}}\\\therefore \,{\rm{d = }}5.95{\rm{ }}x{\rm{ }}{10^{ - 4}}\;m\end{array}\]

21. Kirchhoff's laws in electricity are very useful in solving the complicated circuit connections.

a) What is the significance of first law?

Ans:

The longer is the length of the potentiometer wire, the higher is the accuracy.

b) State and explain second law with circuit diagram.

Ans:

Statement: Kirchhoff's Second Law, also known as Kirchhoff's Voltage Law (KVL), states that the sum of the voltage drops around any closed loop in a circuit must be equal to the sum of the voltage sources in that loop.

Explanation: 

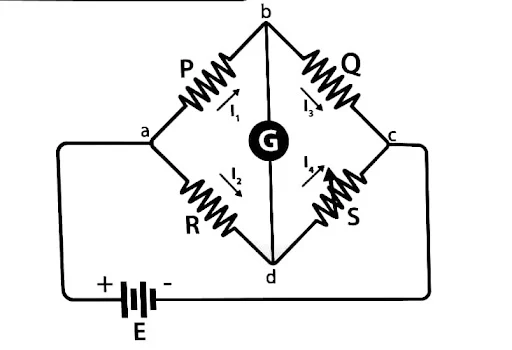
A complex electric circuit is shown in figure. To find the current in various parts of circuit, Kirchhoff’s law can be used. Consider that the direction of emf and current flow in anticlockwise direction is taken as positive and that in clockwise direction as negative. Then applying Kirchhoff’s second law in closed loop ABCFA, we have

$\begin{array}{l}\sum {E = \sum {IR} } \\Or,{\rm{ ( + }}{{\rm{E}}_{\rm{1}}}{\rm{)}} + ( - {E_2}) = ( + {I_1}){R_{\rm{1}}} + ( - {I_2}){R_2}\\Or,{\rm{ }}{{\rm{E}}_{\rm{1}}} - {E_2}{\rm{ = }}{I_1}{R_{\rm{1}}} - {I_2}{R_2}\\Similirly,\;{\rm{ in\; the\; closed\; loop\; FCDEF,\; we\; have\;}}\\\sum {E = \sum {IR} } \\or,{\rm{ ( + }}{{\rm{E}}_{\rm{2}}}{\rm{) + ( - }}{{\rm{E}}_{\rm{3}}}{\rm{) = ( + }}{{\rm{I}}_{\rm{2}}}{\rm{)}}{{\rm{R}}_{\rm{2}}}{\rm{ + ( - }}{{\rm{I}}_{\rm{3}}}{\rm{)}}{{\rm{R}}_{\rm{3}}}\\or,{\rm{ }}{{\rm{E}}_{\rm{2}}}{\rm{ - }}{{\rm{E}}_{\rm{3}}}{\rm{ = + }}{{\rm{I}}_{\rm{2}}}{{\rm{R}}_{\rm{2}}}{\rm{ - }}{{\rm{I}}_{\rm{3}}}{{\rm{R}}_{\rm{3}}}\\At\;{\rm{ the\; junction\; F,\; applying\; krichhoff's\; first\; law,\; we\; have\;}}\\\sum {IR} \\or,{\rm{ ( + }}{{\rm{I}}_{\rm{1}}}{\rm{) + ( + }}{{\rm{I}}_{\rm{2}}}{\rm{) + ( - }}{{\rm{I}}_{\rm{3}}}{\rm{) = 0}}\\{\rm{or, }}{{\rm{I}}_{\rm{1}}}{\rm{ + }}{{\rm{I}}_{\rm{2}}} = {{\rm{I}}_{\rm{3}}}{\rm{ }}\\Solving\;{\rm{ these\;equations,\; we\; can\; calculate\; the\; currents\; }}{{\rm{I}}_{\rm{1}}},{{\rm{I}}_{\rm{2}}}{\rm{ \;and\; }}{{\rm{I}}_{\rm{3}}}.\end{array}$ 

  c) Apply these laws to calculate unknown value of resistance.

Ans:

Kirchhoff’s law can be used to calculate the value of unknown resistance under Wheatstone Bridge.

Kirchhoff’s law can be used to calculate the value of unknown resistance under Wheatstone Bridge.

The current enters the galvanometer and divides into two equal magnitude currents as I₁ and I₂. The following condition exists when the current through a galvanometer is zero,

\(\begin{array}{l}I_{1}P=I_{2}R..(1)\end{array} \)

The currents in the bridge, in a balanced condition, are expressed as follows:

\(\begin{array}{l}I_{1}=I_{3}=\frac{E}{P+Q}\end{array} \)

\(\begin{array}{l}I_{2}=I_{4}=\frac{E}{R+S}\end{array} \)

Here, E is the emf of the battery.

By substituting the value of I₁ and I₂ in equation (1), we get

\(\begin{array}{l}\frac{PE}{P+Q}=\frac{RE}{R+S}\end{array} \)

\(\begin{array}{l}\frac{P}{P+Q}=\frac{R}{R+S}\end{array} \)

\(\begin{array}{l}P(R+S)=R(P+Q)\end{array} \)

\(\begin{array}{l}PR+PS=RP+RQ\end{array} \)

\(\begin{array}{l}PS=RQ..(2)\end{array} \)

\(\begin{array}{l}R=\frac{P}{Q}\times S.. (3)\end{array} \)

Equation (2) shows the balanced condition of the bridge, while (3) determines the value of the unknown resistance.

In the figure, R is the unknown resistance, S is the standard arm of the bridge and P and Q are the ratio arm of the bridge.

d) What is meter bridge? Write name of material used to construct meter bridge.

Ans:

The Instrument based on Wheatstone bridge sed to measure an unknown resistance by comparing it with a known resistance.

Materials Used:  magainin/ constantan/ nichrome/ eureka

OR

a) Derive the expression for impedance in L - C - R circuit.

Ans:

The impedance of an LCR series circuit:

Suppose L be the inductance of the inductor, C be the capacitance of a capacitor and R be the resistance are connected in the series with a.c source having emf. E and frequency f .

And the voltage across the inductor is V_L, the voltage across the capacitor is V_C and the voltage across the resistance.

 

Now the p.d across the inductor having resistance X_L

V_L=IX_L ( in this case V_L lead I by ∏/2)

p.d across the capacitor having the resistance X_C is

V_C=IX_C ( in this case V_C lags the current I by ∏/2)

p.d across the capacitor having the resistance R is

V_R=IR ( in this case V_R and I are in same phase )

Since the inductor, resistor and capacitor are connected in series then the current in all resistance are same but voltage depend upon the resistance i.e. if X_L>X_C then V_L> V_C. then from phasor diagram we have

(OB)²=(OA)²+(BA)²  (by vector sum)

E²=${\rm{V}}_{\rm{R}}^2$+${\left( {{{\rm{V}}_{\rm{L}}} - {{\rm{V}}_{\rm{C}}}} \right)^2}$       from phasor diagram BA=OD= V_L-V_C

Or,E=${\rm{I\: }}\sqrt {{{\rm{R}}^2} + {{\left( {{{\rm{X}}_{\rm{L}}} - {{\rm{X}}_{\rm{C}}}} \right)}^2}} $ from above

Or, Z=E/I =$\sqrt {{{\rm{R}}^2} + {{\left( {{{\rm{X}}_{\rm{L}}} - {{\rm{X}}_{\rm{C}}}} \right)}^2}} $

Where Z=E/I is the impedance of LRC circuit

Phase relation:

From figure we have

$\tan \theta  = \frac{{L\omega  - \frac{1}{{C\omega }}}}{R}$

b) Find the condition of resonance L-C-R circuit.

Ans:

At the resonance the inductance reactance(X _L) is equal to the capacitive reactance X_C i.e.

X_L=X_C

Lω=1/Cω

Or, ω²=1/LC

Or, f=$\frac{1}{{2{\rm{\pi }}\sqrt {{\rm{LC}}} }}$       where ω= 2π f

c) A circuit consists of a capacitor of 2µF and a resistor of 1000Ω. An alternating emf of 12V (rms) and frequency 50 Hz is applied. Find the current flowing, the voltage across capacitor and the phase angle between the applied emf and current.

Ans:

Given,

capacitance, C = 2μF = 2×10^-6 F

resistnce , R = 1000 Ω
alternating emf, V = 12 V
frequency, f = 50 Hz
voltage across capacitor, V_C = ?
phase angle between the applied emf and the current, φ = ?

Now, the current in this circuit is given by the expression \[I=\frac{V}{\sqrt{R^2+ X_C^2}}\] Here, \[\begin{align*} X_C&=\frac{1}{\omega C}\\ &=\frac{1}{2 \pi f C}\\ &=\frac{1}{2 \times \pi \times 50 \times 2 \times 10^{-6}}\\ &=1591.55 \hspace{0.1cm} \Omega\\ \end{align*}\] Then, \[\begin{align*} I&=\frac{V}{\sqrt{R^2 + X_C^2}}\\ &=\frac{12}{\sqrt{(1000)^2 + (1591.55)^2}}\\ &=0.0064 \hspace{0.1cm} \text{A}\\ \end{align*}\] Also, \[\begin{align*} V_C&=I\times X_C\\ &=0.0064 \times 1591.55\\ &=10.2 \hspace{0.1cm} \text{V}\\ \end{align*}\] The phase angle between the applied emf and the current is, \[\begin{align*} tan\phi&=\frac{X_C}{R}\\ \phi&=tan^{-1} \frac{1591.55}{1000}\\ \therefore \phi&= 57.9^\circ\\ \end{align*}\]
Thus, the voltage across capacitor is 10.2 V and the phase angle is 57.9⁰

22. a) State Bohr's postulate of atomic model.

Ans:

Postulates of Bohr’s theory are:

1. Electron revolves around the nucleus in certain permitted orbits called radii.
2. Each energy level has a specific energy associated with it, and electrons can only move from one energy level to another by absorbing or emitting energy in the form of photons.

b) Derive an expression for radius of n^th orbit in H-atom.

Ans:

So by Bohr’s postulates we have,
Angular momentum has to be equal to $n\times \dfrac{h}{2\pi }$ , that is,
$mvr=\dfrac{nh}{2\pi }$
Where ‘n’ can be= 1, 2, 3…
m=mass of the electron
v= velocity of the electron
r=radius of the orbit
$v=\dfrac{nh}{2\pi mr}$ ………………… (1)
Also we have, the centripetal force should be equal to the force of attraction between nucleus and electron, for this is the force that balances the centripetal force and hence the electron continues its revolution around the nucleus. So we have,
$\dfrac{m{{v}^{2}}}{r}=\dfrac{K{{Z}^{2}}{{e}^{2}}}{{{r}^{2}}}$ ……………………. (2)
Where, K is the Coulomb constant =$K=9\times {{10}^{9}}N.{{m}^{2}}.{{C}^{-2}}$
e = charge of an electron
Z= atomic of number of the atom
Substituting (1) in (2), we get,
$\begin{align}
  & \dfrac{m{{n}^{2}}{{h}^{2}}}{4r{{\pi }^{2}}{{m}^{2}}{{r}^{2}}}=\dfrac{K{{Z}^{2}}{{e}^{2}}}{{{r}^{2}}} \\
 & \Rightarrow r=\dfrac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}mKZ{{e}^{2}}} \\
\end{align}$
Here in the question, we have been asked for the radius of nth orbit of a hydrogen atom specifically. As we know the atomic number (Z) of a hydrogen atom is 1, we can substitute this value for Z.
So we get the required relation as,
$r=\dfrac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}mK{{e}^{2}}}$

c) Calculate de Broglie wavelength of electron when it is accelerated by 500 volts. (mass of electron 9.1 * 10^-31 kg, Planck's constant 6.62 x 10^-34Js, charge of electron 1.6 x 10^-19C)

Ans:

$\begin{array}{l}\lambda  = \frac{h}{{\sqrt {2mE} }} = \frac{h}{{\sqrt {2mqV} }}\\or,{\rm{  }}\lambda  = \frac{{6.6 \times {{10}^{ - 34}}}}{{\sqrt {2 \times 9.1 \times {{10}^{ - 31}} \times 1.6 \times {{10}^{ - 19}} \times 50} }}\\\therefore {\rm{ }}\lambda  = 1.72 \times {10^{ - 10}} = 1.72A\;\end{array}$

OR

Radio activity is the spontaneously occurring phenomenon in nature.

a) What is radio activity?

Ans:

The process by which an unstable nucleus becomes stable by emitting radiations like α, β and ϒ radiations is called radioactivity.

b) Obtain N = N₀e^-λt) in radioactive decay law.

Ans:

Let us consider at time t=0, a radioactive sample contains N_o number of atoms and after time t, N number of atoms are left due to disintegration of the atoms. Further let us consider that dN number of atoms disintegrate in time between t and t+dt. Then rate of disintegration at time t will be $\frac{{dN}}{{dt}}$.

According to decay law,

$\frac{{dN}}{{dt}}$ α N  

or, $\frac{{dN}}{{dt}}$ =-λN………………..(1)

Where λ is proportionality constant called as disintegration constant or decay constant. The –ve sign

indicates that the no. of atoms N decreases as time increases. The rate of disintegration $\frac{{dN}}{{dt}}$  is called the activity of the radioactive sample.

Equation (1) can be written as

$\frac{{dN}}{{dt}} = {\rm{  - }}\lambda {\rm{t}}$

Integrating the equation on both sides, we get
$\begin{array}{l}\int_{{N_0}}^N {\frac{{dN}}{{dt}}}  = \int_0^t {{\rm{ - }}\lambda } t\\or,{\rm{ }}\;{\rm{[ln N]}}_{{N_0}}^N = {\rm{ - }}\lambda [t]_0^t\\or,{\rm{ ln N  -  ln }}{N_0}{\rm{  =   - }}\lambda (t - 0)\\or,{\rm{ ln }}\frac{N}{{{N_0}}}{\rm{  =   - }}\lambda t\\or,{\rm{  }}\frac{N}{{{N_0}}}\,{\rm{ =  }}{{\rm{e}}^{{\rm{ - }}\lambda t}}\\or,\;{\rm{ }}N{\rm{  =  }}{N_0}{{\rm{e}}^{{\rm{ - }}\lambda t}}\end{array}$
This equation is known as decay equation. It shows that the decay of radioactive atoms obeys exponential law.

c) Describe the significance of decay curve showing the longest lifetime of radioisotopes.

d) The half-life of radium is 1620 years. After how many years 25% of a radium block remains undecayed?

Answer:

Let initial amount of radium=N₀

Half-life of radium=1600 years

The quantity left after n half-lives=N=25% of ${N_0} = \frac{1}{4}{N_0}$

The amount of radioactive element after n half-life is given by

$N = {N_0}{\left( {\frac{1}{2}} \right)^n}$

Where n=Number of half lives

N₀=Initial amount of radioactive element

N=Amount left of radioactive element after n half lives

Substitute the values then we get

$\begin{array}{l}\frac{{{N_0}}}{4} = {N_0}{\left( {\frac{1}{2}} \right)^n}\\{\left( {\frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^n}\end{array}$

When base are equal on both sides of equal to then power will be equal therefore,

n=2

Time of disintegration=No. of Half-lives x Half Life

Time of disintegration=1600 x 2 =3200years