Subject: Physics (1021 D3)
Group A
Multiple Choice Question [11 x 1 =11]
Rewrite the correct option in your answer sheet.
1. Which quantity in rotational motion is analogous to
velocity in linear motion?
a. Torque
b. Moment of inertia
c. angular momentum
d. angular velocity
Solution: d. Angular Velocity
2. Two capillary tubes A and B of radii 0.4 cm and 0.8 cm
are dipped in the same liquid. What is the ratio of heights through which
liquid rises in the tubes A and B?
a. 1:2
b. 2:1
c. 1:4
d. 4:1
Solution: b. 2:1
3. If T is the time period of simple pendulum, then what
will be its value when the effective length is doubled?
a. T
b. T/2
c. T/√2
d. 2T
Solution: c. T/√2
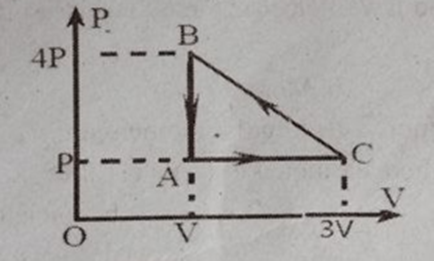
4. Find out the work done in the closed loop ACB from the graph
a. 12PV
b. -12PV
c. +3PV
d. -3PV
Solution:
c +3PV
5. When the door of a refrigerator is left open in a room,
the temperature of the room
a. increases
b. decreases
c. remains same
d. first increases then decreases
Solution:
a increases
6. If the pressure amplitude of a sound wave is halved then
intensity of s wave changes by a factor of
a. 2
b.1/2
c. 4
d. ¼
Solution: d ¼
7. At polarizing angle, the angle between reflected and
refracted rays is
a. 0°
b. 45°
c. 60°
d.90°
Solution: d.90°
8. When a difference of temperature is maintained across a
single conductor and a current is passed through it; heat is either evolved or
absorbed. effect is called?
a. Seebeck effect
b. Peltier effect
c. Thomson's effect
d. Joule's effect
Solution: c. Thomson Effects
9. The current in a wire increases from A to B
then the direction of induced current in the coil is
a. clockwise
b. anticlockwise.
c. no current is induced
d. alternating current
Solution: b. anticlockwise
10. Kirchhoff's second law of electric circuit is based on
principle of conservation of
a. Charge
b. Mass
c. Linear momentum
d. Angular momentum
Solution: Kirchhoff’s Second Law is based on conservation
of Energy.
[Note: Answer is not given in
option. May be an Error in Question paper]
11. The point from where earthquake start's is called....
a. Hypocenter
b. epicenter
c. Dip
d. focus
Solution: a. Hypocenter
Group B
Group B: Short Answers Question
12. a. Define Simple harmonic motion. Give its two examples.
b. In a laboratory experiment with a simple pendulum, it
was found that it took 18 seconds to complete 10 oscillations when the
effective length was kept at 80 cm. Calculate the acceleration due to gravity
from these data.
Solution:
(a) Simple harmonic motion (SHM) is a type of oscillatory motion in
which an object moves back and forth repeatedly along a straight line, with a
restoring force that is proportional to its displacement from a fixed point.
Example: Motion of Pendulum and Motion of mass attached to Spring.
(b)
Given:
Length(l) = 80cm = 80 × 10 -2m
Number of Oscillations: (n1) = 10
Time taken for single Oscillation (T) =$18/10$= 1.8 Sec
We Know,
$T = 2\pi \sqrt{\frac{l}{g}}$
Or, $1.8\text{ s} = 2\pi\sqrt{\frac{80\times10^{-2}\text{
m}}{g}}$
Or, $\sqrt{\frac{80\times10^{-2}\text{ m}}{g}} =
\frac{1.8\text{ s}}{2\pi}$
Squaring both sides:
$\frac{80\times10^{-2}\text{ m}}{g} = \left(\frac{1.8\text{
s}}{2\pi}\right)^2$
Solving for $g$:
$g = \frac{80\times10^{-2}\text{ m}}{\left(\frac{1.8\text{
s}}{2\pi}\right)^2} \approx 9.7 \text{ m/s}^2$
Therefore, the value of acceleration due to gravity is
approximately 9.7 m/s2.
OR
a. Define radius of gyration. Write its expression for a
thin rod about an axis passing through center and perpendicular to its length.
b. The flywheel of an engine has a moment of inertia 2.5
kgm² about its rotation axis. Calculate: Torque required to bring it up to an
angular speed of 400 rev/min in 8 second starting from rest and final kinetic
energy of fly wheel.
Solution:
(a) The radius of gyration is a measure of the distribution of mass around
an axis of rotation. It is the distance from the axis of rotation to a point
where the entire mass of the body could be considered to be concentrated, such
that the moment of inertia of the body about that axis would remain the same.
The radius of gyration of a thin
rod about an axis passing through its center and perpendicular to its length is
$l/\sqrt{12}$ or $l/(2\sqrt{3})$.
(b)
Given:
Moment of Inertia (I)=
Frequency(f) =400rev/min = 400/60
= 20/3
Time taken (t)= 8seconds
Now,
$\begin{array}{l}Torque(\tau ) = I\alpha \\ = 2.50 \times
\frac{\omega }{t}\\ = 2.50 \times \frac{\omega }{t}\\ = 2.50 \times \frac{{2\pi
f}}{t}\\ = 2.50 \times \frac{{2\pi
\times \frac{{20}}{3}}}{8}\\ = 13.08N.m\end{array}$
13. a. Small air bubbles rise slowly while big bubbles
rise rapidly through the liquid, why?
b. Water flows in a horizontal tube as shown in figure below. The pressure of water changes by 600N /m2 between A and B where the area of cross section are 30cm2 and 15cm2 respectively. Calculate the rate of flow of water through the tube.
Solution:
(a) When it comes to bubbles in a liquid, their size
plays a crucial role in determining their speed of ascent. Smaller bubbles tend
to move slowly because their terminal velocity is quite low, whereas larger
bubbles move rapidly owing to their high terminal velocity. As a result, a
small bubble will take longer to rise through a liquid compared to a larger one
that will ascend quickly.
(b)
Let the velocity at A = vA and that at B = vB.
We Know,
From Equation of Continuity: $V_B / V_A = 30/15 = 2$
From Bernoulli’s equation,
$\begin{array}{l}{P_A} + \frac{1}{2}\rho {V_A}^2 = {P_B} +
\frac{1}{2}\rho {V_B}^2\\Or,{\rm{ }}{P_A} - {P_B} = \frac{1}{2}\rho ({V_B}^2 -
{V_A}^2)\\Or,{\rm{ }}600 = \frac{1}{2} \times 1000[{(2{V_A})^2} -
{V_A}^2]\\Or,600 \times \frac{2}{{1000}} = 3{V_A}^2\\Or,{\rm{ }}{V_A}^2 =
0.4\\Or,\;{V_A}{\rm{ =
0}}{\rm{.632}}\end{array}$
The rate of flow = (30cm2)(0.63m/s)=1800cm3/s.
14. a. A thermos bottle containing coffee is vigorously
shaken. Considering the coffee as a system:
i. Does its temperature rise?
ii. Has its internal energy changed?
b. A quantity of monoatomic gas at 27°C is compressed
adiabatically to 8/27 of its volume. Find the change in temperature assuming γ
to be 1.66.
Solution:
(a) i) Yes, the temperature will increase slightly.
ii) As thermos
flask is insulated, so no heat energy added to the system, △Q=0
Work is done on the system by shaking it against viscous
force. Hence △w=−ve
Internal energy =△U=△Q−△w=0−(−△w)⇒△U=+△w
△U=+ve
So, the temperature of the system will increase due to
increase in internal energy.
(b)
Given:
T1 = 27oC=300K
γ= 1.66
Let the initial volume of the gas be V i.e V1=V
Thus final volume of gas (V2)= $\frac{8}{27}$
We Know,
TV γ-1=Constant
So,
15. a. In Young's double slit experiment, no interference
pattern is detected when two coherent sources are infinitely close to each
other. Justify.
b. A parallel beam of monochromatic light falls on a
single slit 1 mm wide. When the diffraction pattern is observed on a screen 2 m
away, the central band is to have a width of 2.5 mm. Find the wavelength of
light.
c. Diffraction pattern cannot be achieved from a wide
slit illuminated by monochromatic light. Justify.
Solution:
(a) The fringe width in a
double-slit interference pattern is inversely proportional to the distance
between the two slits. When the distance between the slits is very small, the
fringe width becomes very large. In this case, a single fringe may occupy the
entire field of view, making it difficult to detect the interference pattern.
Therefore, when two coherent sources are placed extremely close to each other,
no interference pattern is observed.
(b)
Given:
Distance between slits(d)=1mm=10-3m
Distance between Screen and Slits (D) = 2m
Band Width (β) = 2.5mm =2.5×10-3m
We Know,
Thus, the wavelength of light is 1.25 ×10-6m
(c) When a beam of light
passes through a wide slit, where the width of the slit (a) is much larger than
the wavelength of the light (λ), the bending of light due to diffraction will
be very small and almost negligible. As a result, the diffraction pattern
produced on a screen placed behind the slit will not be observable.
OR
a. Construct spherical and plane wave front.
b. Use Huygens's principle to verify the law of
refraction of light.
Solution:
(a)
|
Spherical wave
front |
Plane wave front |
|
|
|
(b)
Let us consider a plane wave front AP incident on a reflecting surface XY at an angle of incidence i. SA and QP are the incident rays perpendicular to AP.
At first the wave front arrives at point A and then at
B,C,D.....of the reflecting surface .Thus different point on the surface XY
becomes source of secondary wavelets at different instant of time.
When the disturbance from point P on the incident wave front reaches at point E
on the reflecting surface, the secondary wavelets from the point A,B,C,D on the
reflecting surface have acquired radius AA',BB',CC' and DD' respectively. The
tangent plane A'E touching all the secondary wavelets represent reflected wave
front and the lines A'R' and ER perpendicular to the reflected wave front
represents reflected rays.
Therefore, N'ER= r = angle of reflection
Now in right angled triangles APE and AA'E
i) AA'=PE (Distance traveled by light in same time)
ii) AA'E=APE=90°
iii) AE=AE is common side.
Hence the triangles are congruent therefore,
Tr. PAE= Tr. AEA'
Or, i = r
This verifies the law of reflection
Further if we consider the incident plane of wave front is
parallel to the plane of paper, the plane of reflected wave front and plane of
normal all lie in that plane. So, the incident ray normal to the reflecting
surface and the reflected ray all lie in the same plane. This proves another
law of reflection.
16. a. State Ampere's Circuital law.
b. Define one ampere current on the basis of force
between two parallel current carrying conductors.
c. The hysteresis curve between soft iron and steel is given below in the figure.
i. Which has low
retentivity between soft iron and steel?
ii. Which has low hysteresis loss between two? Why?
Solution:
(a) Ampere's Circuital law states that, “the line
integral of the magnetic field around any closed path in free space is equal to
µ0
times the total current enclosed by the path.”
\[\oint {\mathop B\limits^ \to } .d\mathop l\limits^ \to = {\mu _0}I\]
(b) One ampere is that current following in each of two
infinitely long parallel conductors 1 meter apart such that the force permitter
length on each conductor is 2×10-7N.
(c) i. Steel has more coercivity and less
retentivity compared to soft iron.
ii. Soft iron has less hysteresis losses than
steel, Because soft irons has low coercivity and high retentivity as compared
to steel.
17. a. State and explain Faraday's laws of
electromagnetic induction.
b. If the transformer ratio is less than one, which
transformer is this a how?
c. What emf will be induced in a 10 H inductor in which
current changes from 10 A to 7 A in 9×10-2 S?
Solution:
(a) Faraday’s Law of
electromagnetic induction is given as:
- When magnetic flux linking a coil changes, an e.m.f. is induced in it.
- This induced e.m.f. lasts so long as the change in magnetic flux continues.
- The induced e.m.f. in the coil is directly proportional to the rate of change of flux linkages.
(b) It is a step-down
transformer. As, Ns/Np is known as the turn’s ratio. In step down transformer
the number of turns in secondary winding (Ns) will be less than the number of
turns in primary (Np).
(c)
Given:
L=10H
I1=10A
I2=7A
dt=9 × 10-2S
We Know,
E.M.F. (E) = $\frac{{LdI}}{{dt}}$
$\begin{array}{l} \Rightarrow E =
\frac{{ - L({I_2} - {I_1})}}{{dt}}\\ \Rightarrow E = \frac{{ - 10(7 - 10)}}{{9
\times {{10}^{ - 2}}}} = 333.33V\end{array}$
18. a. State and explain
Bohr's Postulates.
b. The ionization potential of
hydrogen is 13.6 V. What does it mean?
c. Electrons are accelerated
from rest through a potential difference of 1000 volts in an X-ray tube.
Calculate the minimum wavelength of X-radiation generated. (Given, Charge on an
electron 1.6×10-19 C. Planck's constant = 6.62 × 10
-34 Js )
Solution:
(a) Postulates of Bohr’s Model
of an Atom
- Electrons orbit around the nucleus in circular paths
called shells.
- Each shell has a fixed energy and is represented by a
quantum number (n=1, 2, 3...).
- The lowest energy level is assigned as K-shell and
higher levels as L, M, N, etc.
- Electrons can move between shells by gaining or
losing energy.
- When an electron is in the lowest energy level, it's
called the ground state.
(b) The ionization
potential of hydrogen is 13.6 electron volts (eV), which means that an electron
in a hydrogen atom requires at least 13.6 eV of energy to be removed from the
atom.
(c) If electrons are accelerated to a velocity v by a potential difference V and then allowed to collide with a metal target, the maximum frequency of the X-rays emitted is given by the equation:
\[\begin{array}{l}{\lambda _{\min }} = \frac{{hc}}{{mV}}\\{\lambda _{\min }} = \frac{{6.62 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{{1.6 \times {{10}^{ - 19}} \times 1000}} = 1.24 \times {10^{ - 9}}\end{array}\]
19. a. (i) A decay curve is given in the figure below.
If No and N represents numbers of atoms
presents in a sample initially and after time t respectively. What will be the
number of atoms decayed from the sample after fifth half-lives?
b. What is the value of C if B is the second half life?
c. A radioactive nucleus undergoes a series of decay
according to the scheme.
\[A\mathop \to
\limits^\alpha {A_1}\mathop \to \limits^{\beta - } {A_2}\mathop \to \limits^\alpha {A_3}\mathop
\to \limits^\gamma {A_4}\]
If the mass number and atomic number of A are 180 and 72
respectively. What are these numbers for A2 and A4?
Solution:
(a)
(b)
(c) As we know, mass and charge of
α=4 and +2
β=0 and −1
γ=0 and 0
\[\begin{array}{l}So,\;{\rm{ }}A\mathop \to \limits^\alpha {A_1}\mathop
\to \limits^{\beta - }
{A_2}\mathop \to \limits^\alpha {A_3}\mathop
\to \limits^\gamma {A_4}\\m{\rm{ \;\;\;180\;\;
\; \; 176\; \;\;176\;\;\; 172\;\;\;\;172\;}}\\{\rm{e\;\;\;
\;\; 72\;\;\;\; \;\; 70\; \; \; \;\; 71\;\;
\;\;\;69\;\; \;\;\;\;\;69\;\;}}\end{array}\]
So,
Mass and charge of A3 is 172 &169
Mass and charge of A4 is 172 & 69.
GROUP C
Give long answers to the following questions.
20. a. Where will a man hear louder sound at node or
antinode in a stationary wave? Justify.
b. A stretched string of length 1 m and mass 5 x 10 -
4 kg fixed at both ends is under the tension of 20 N. It is plucked at a
point situated at 25 cm from one end. What would be the frequency of vibration
of the string?
c. A person sitting on the railway station feels
increasing pitch of railway engine as the train approaches to him, why?
d. Is it possible to create longitudinal wave in spring?
How?
Solution:
(a) At the antinodes, strain is minimum. At the nodes
strain is maximum. So, variation of pressure is maximum at the nodes. Hence a
loud sound is heard at the node.
(b) At 25cm , there will be antinode . So ,
wire will vibrate in two loops.
(c) The pitch of a sound
is related to its frequency, which is the number of waves or vibrations per
second. As the train approaches the person sitting on the railway station, the
sound waves produced by the train are compressed or "squeezed" by the
train's motion towards the person. This results in an increase in the frequency
or pitch of the sound waves that reach the person's ears.
(d) A longitudinal wave can be set up in a stretched spring by compressing the coils in a small region and releasing the compressed region. The disturbance will proceed to propagate as a longitudinal wave along the length of the spring. It is quite possible to set up a transverse wave in the spring, simply by displacing a section of the spring in a direction perpendicular to its length and releasing it.
21. a. A potentiometer is preferred to a voltmeter.
Justify.
b. In the circuit shown in figure, using Kirchhoff's
laws, find
i. the current in the R3 resistor,
ii. the unknown resistance R3
iii. the unknown emf E2.
c. In the graph below,
i. What are the temperature at points A and B called in
thermoelectric effect?
ii. If θc= 00C and temperature at point B is 500°C. Find the temperature at point A?
Solution:
(a) The potentiometer is
preferred over voltmeter for measurement of emf of cell because the
potentiometer does not draw any current for itself from the primary circuit. Therefore,
it gives more accurate measurement thereby acting as an ideal voltmeter.
(b)
(c) i. Temperature at point A is called neutral Temperature
and Temperature at point B is Inversion temperature and denoted by θn
and θi respectively.
ii. We know that θn(A) $= \frac{{{\theta
_c} + {\theta _i}(B)}}{2}$
$\begin{array}{l} = \frac{{0 + 500}}{2}\\ = 250\end{array}$
OR
a. Sketch a graph showing the variation of capacitive
reactance with the frequency of AC mains.
b. A Capacitor blocks DC. Justify.
c. A series L-C-R circuit consists of a resistor of 50 Ω,
an inductor of 10mH and a capacitor of 100µF. It is connected across a
200 V, 50 Hz a.c. supply.
Calculate:
i. impedance of the circuit
ii. Power factor of the circuit
iii. Voltage across an inductor.
d. Discuss a.c. through a series circuit of resistance
and inductance with the help of phasor diagram.
Solution:
(a)
(b) Because the capacitor's electrode plates are
separated by an insulator (air or a dielectric), no DC current can flow unless
the insulation disintegrates.
(c)
Resistance (R)=50 Ω
Inductance (L)=10mH=10×10-3H=10-2H
Capacitance (C) = 100µF=10-4F
Potential(E)=200V
Frequency (f)=50Hz
Calculating:
ω = 2πf=100π
XL=Lω=10-2×100π= π
XC=Cω=10-4×100π=10-2π
I=V/R=200/50=4
Now,
(i) Impedance (Z)= $\sqrt {{R^2} + {{({X_L} -
{X_C})}^2}} $
$\begin{array}{l} = \sqrt {{{50}^2} + {{(\pi - {{10}^{ - 2}}\pi )}^2}} \\ =
50.096\end{array}$
ii. Power factor $ = {\mathop{\rm Cos}\nolimits}
\theta = \frac{R}{{\sqrt {{R^2} +
{{({X_L} - \frac{1}{{{X_C}}})}^2}} }}$
$\begin{array}{l} = \frac{{50}}{{\sqrt {{{50}^2} +
{{(\pi - \frac{1}{{{{10}^{ - 2}}\pi
}})}^2}} }}\\ = 0.86\end{array}$
iii. Voltage across an inductor=$IX_L$=4π
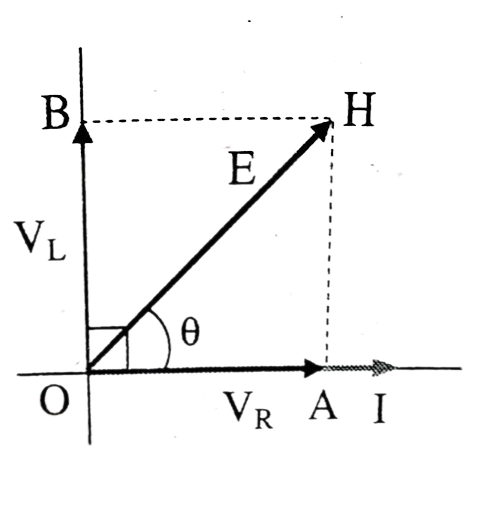
(d) Suppose a pure resistance R and a pure inductance L is connected in series to a source of alternating e.m.f. shown in a figure. Let E be the r.m.s value of applied alternating e.m.f. and I be the r.m.s value of current flowing in the circuit.
The potential difference across the inductor, $V_L = IX_L$ (leads current I by an angle of π/2).
The potential difference across R, $V_R = I.R.$ (in phase with the current).
Since $V_R$ and I are in phase so $V_R$ is represented by OA in the direction of I. the current lags behind the potential difference $V_L$ by angle of $\frac{\pi }{2}$ so $V_L$ is represented by OB perpendicular to the direction of I. So the resultant of $V_R$ and $V_L$ is given by OH. The magnitude of OH is given by
\begin{align*} OH &= \sqrt {OA^2 + OB^2} = \sqrt {V_R^2 + V_L^2} \\ \text {or,} \: E &= \sqrt {I^2R^2 + I^2X_L^2} \\ \text {or,} \: E &= I\sqrt {R^2 + X_L^2} \\ \text {or,} \: \frac EI &= \sqrt {R^2 + X_L^2} \\\end{align*}
But \(\frac EI = z\), is effective opposition of L-R circuit to a.c. called impedance of LR circuit. The impedance of L-R circuit is given by
$\begin{array}{l}Z = \sqrt {{R^2} + X_L^2} \\Again,\\I = \frac{E}{Z} = \frac{E}{{\sqrt {{R^2} + X_L^2} }}\\\therefore I = \frac{E}{{\sqrt {{R^2} + {{(L\omega )}^2}} }}\left[ {{X_L} = L\omega } \right]\end{array}$Let θ be the angle between E and I, so from figure, We have:
$\begin{array}{l}\tan \theta = \frac{{{V_L}}}{{{V_R}}} = \frac{{I{X_L}}}{{IR}}\\or,\,\tan \theta = \frac{{{X_L}}}{R}\\\therefore \tan \theta = \frac{{L\omega }}{R}\end{array}$
If the values of $X_L$ and R are known as θ can be calculated. Current lags behind applied voltage or e.m.f.