Interference of Light Note | Class 12 Physics | NEB | NEPALI EDUCATE

Interference:
The phenomenon of re distribution of light energy in a medium due to superposition of two light waves from the coherent source is known as interference.
The interference pattern of light is produced when two light waves of the same amplitude, same wavelength, same frequency and same phase or constant phase difference travelling in a same medium in the same direction supreme pose each other.

Types of interference:
There are two types of interference patterns. They are constructive interference and destructive interference.
i. Constructive interference:
When two waves supreme pose each other in the same phase a bright point of a maximum intensity is obtained is called constructive interference.

ii. Destructive interference:
When two waves supreme pose each other in different phases or a dark point of minimum intensity is obtained is called distractive interference.

Coherent sources:
The two sources of a light which emit light waves continuously have the same amplitude, same wavelength, same frequency and same phase or a constant phase difference are known as coherent sources. In real practice no independent two sources are coherent in nature. To realize coherent source in real life we kept double slit S₁ and S₂ in front of a monochromatic source. Now the slit S₁ and S₂ behave like coherent source.

Theory of interference:
Let us consider light waves from coherent sources having displacement y₁ and y₂ travelling in the same medium in the same direction super impose each other to produce interference patterns.
y₁=rsin ωt ........(i)
y₂=rsin (wt + Φ) ....(ii)

We have,
From the principal of superposition
y= y₁ + y₂
y= rsin ωt + rsin (wt + Φ)

y= 2rcos (  ). Sin (wt +   )

y=A Sin (wt +   ) …………………. (iii)

where, A= 2rcos (  )

From equation (iii)

For Maximum Intensity:

A = ± 2r,

if cos (  ) =1

i.e. cos (  ) =cos nπ; n=0,1,2,3, ……

à Φ = 2nπ ……….(iv)

Also,

Φ =  x

àx=n λ ……(v)

For Minimum Intensity:

A=0, for Cos () =0

Or, Cos () = Cos (2n+1)

Or, Φ = (2n+1) π……….(vi)

Also,

x= (2n+1) 

We Know,

I ∝ (amplitude)²àI ∝ A²

I=4r²Cos² () ……. (viii)
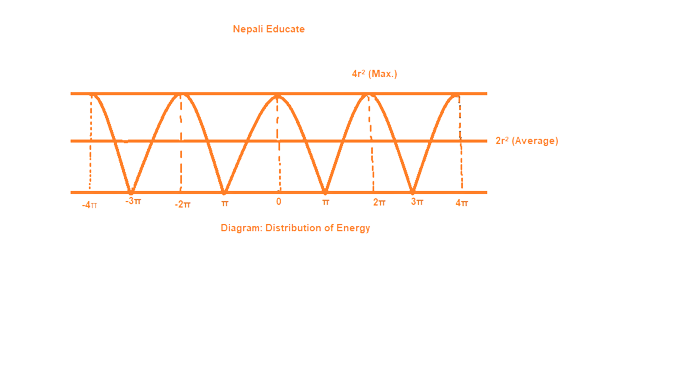
It shows that the intensity of the resultant wave depends upon phase and fluids between maximum and minimum as shown in the graph.

The average energy of a wave after interference is 2 r² which is equal to the energy of the Waves before interference. There is only change in distribution of energy the energy at the dark point is shifted to the bright but Total energy remains conserved.

Young's double slit experiment:
In 1801 Thomas Young established the wave nature of light by proving that the light waves interfere with each other. His experimental consists of a monochromatic source of light(S) kept in front of a double slit S₁ and S₂. The screen is placed at some distance from the double slit to observe the interference pattern.

Two light waves from the slate S₁ and S₂ meet at the center of the screen in such a way that their path difference is zero. As a result, a bright pattern is obtained at the center of the screen called Central Maxima or zeroth maxima. This Central pattern is followed by an alternative dark and bright pattern on either side.

Derivation:
Suppose the light waves from the slate S₁ and S₂ meet at any point P on the screen. Point p will be either maxima or minima depending on the path difference.

Where,
D is the distance between source and screen,
d is separation of sheet and
y is the position of the pattern from the center of the screen.

From the figure,
Path difference, (∆x) = S₂P₁ - S₁ P₁.......(1)

In ∆S2PN:
S₂P² =D²+ (y+d/2)².......(2)

In ∆S1PM,
S₁P²= D²+ (y-d/2)².............(3)
Solving equation 2 and 3,
S₂P²-S₁P²=2yd
(S₂P-S₁P)(S₂P+S₁P)=2yd
(S₂P-S₁P)=2yd/(S₂P+S₁P)
(S₂P-S₁P)=2yd/2D             [∵, S₁P ≈ S₂P ≈ D]
Thus, x = yd/D..........(4)

For Maxima:
x = n λ and from equation 4,

i.e., n λ = yd/D

or, y= n λD/d

Put n=2 and n= 1and subtract.

β_bright=y₂-y₁ = λD/d ………………. (5)

Where, β_bright is the distance between two consecutives bright pattern.

For Minima:
x=(2n+1)  and from equation 4,

i.e., (2n+1)= yd/D

or, y=(2n+1) 

Put n=2 and n= 1and subtract.

β_dark=y₂-y₁ = λD/d …… (6)

Where, β_dark = is the distance between two consecutives dark pattern.

From equation 5 and 6 it is clear that the wheats of bright and dark patterns during interference are equal called fringe width.

Optical path
The optical path of the medium is defined as the equivalent distance that travels by light in vacuum during the same time for which it travels in medium. Mathematically it is given by the relation

Optical path (L) = μd
Where,

μ =   refractive index of medium and
d = distance travelled by the light in a medium.

Effect of Insertion of Denser Medium:
L=Optical Path in air + Optical path in medium

i.e. L =(d-t)+ μt

i.e. L =d+( μ-1)t

Eg:

Interference fringes were produced by the young slit method the wavelength for light being 6×10^-7 m. When a film of a material 3.6 ×10^-3 cm thick was placed over one of the slits, the Fringes pattern was displaced by a distance equal to 30 times that placed between two adjacent fringes. Calculate the μ of the material.
Here,
λ = 6×10^-7

t= 3.36×10^-3cm = 3.36×10^-5m

n=30;
Now,
nλ = (μ-1) t
μ=1.5